Задача №5. Найти следующие пределы, используя правило Лопиталя
Найти следующие пределы, используя правило Лопиталя. 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11)
Решение задачи №1
Для решения примеров на вычисление производной необходимо выучить наизусть правила дифференцирования, таблицу производных, а также нужно хорошо разбираться в порядке следования операций в математическом выражении. Весь этот материал изложен в лекции 1, где также вычислено большое число производных и приведены замечания, полезные при дифференцировании. 1) 2)
3)
4)
5) 6)
7)
8)
9)
10)
11)
12)
13)
14)
15)
16)
Решение задачи №2
Примеры 1) и 2) связаны с вычислением производной функции, заданной неявно. Именно, если независимая переменная 1) Дифференцируем обе части уравнения
2)
12) Рассмотрим систему Находим Получаем: Ответ:
13) Пусть Получаем:
Ответ:
Решение задачи №3
1) Область определения функции
Итак, у функции существуют и левосторонний предел Рассмотрим точку
Значение функции в точке Итак, функция непрерывна на множестве
2) Область определения функции
Поэтому точка Итак, функция непрерывна на множестве 3) Область определения функции Найдем односторонние пределы функции в точке
Итак, точка Рассмотрим точку
Итак, точка Таким образом, функция непрерывна на множестве 4) Область определения функции
Итак, точка Функция непрерывна на множестве
Решение задачи №4
Перед решением примеров данного раздела следует изучить лекции 4 и 5. 1)
2) Вычислим отдельно предел числителя и знаменателя. Имеем:
Поэтому, из соотношения (12) на стр.20 получаем:
3) По теореме 6 на стр. 18 при
4) Из цепочки эквивалентностей (8) на стр. 17 получаем
5) Решение этого примера аналогично решению примера 4. При
6) При
7) Имеем: В процессе решения мы применили эквивалентность 8) Здесь имеет место неопределенность
9) Разделив и умножив дробь на сопряженные выражения для числителя и знаменателя, получаем:
10) Решение этого примера совершенно аналогично решению примера 3. А именно, используя эквивалентность (9), получаем:
11) Сперва применяем формулу преобразования суммы синусов в произведение, а затем используем 4–е свойство предела функции (стр.13):
12) Решение аналогично решению примеров 3 и 10:
13) В процессе решения мы применили эквивалентность 14) Перед решением этого примера следует просмотреть пример 19 на стр. 22. Обозначим
Решение задачи №5
Для решения примеров этого раздела необходимо изучить теорему Лопиталя (см. теорему 9 на стр. 20-21). Правило Лопиталя применяют повторно, пока не устранится неопределенность или обнаружится, что нужные пределы не существуют. 1) 2) 3) 4) 5) 6) 7)
8) 9)
10) 11) Обозначим
Окончательно:
|

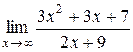




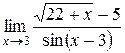

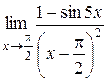



 .
.

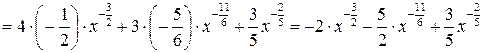 .
.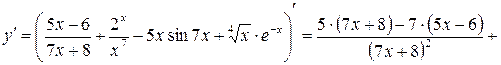

 .
.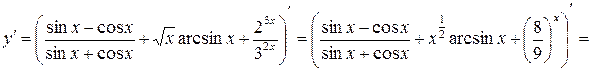


 .
. .
.
 .
.
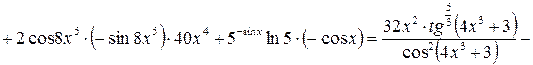
 .
.
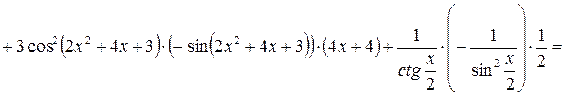
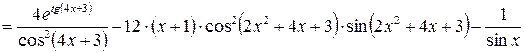 .
. .
. .
.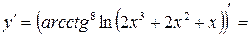

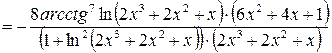 .
.

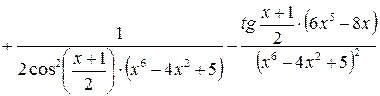 .
.


 .
.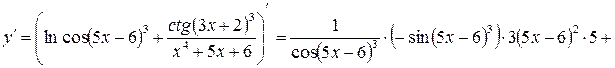
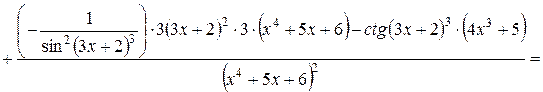
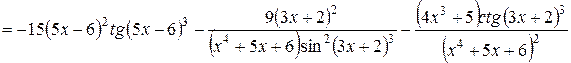 .
.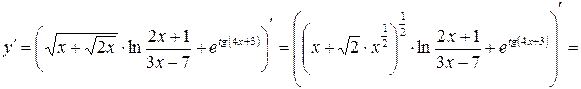
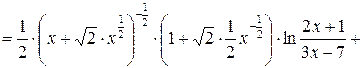
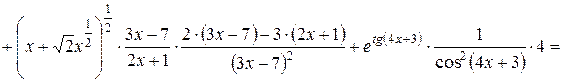
 .
.


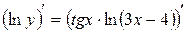
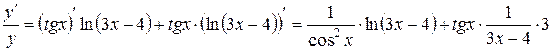
 .
.
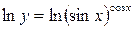




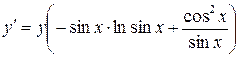
 .
. и функция
и функция  связаны уравнением вида
связаны уравнением вида  , которое не разрешимо в явном виде относительно
, которое не разрешимо в явном виде относительно  , то
, то  .
.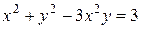 по переменной
по переменной 

 .
.



 .
. , где
, где 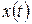 и
и  – дифференцируемые функции и
– дифференцируемые функции и  , определяет
, определяет 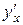 существует и вычисляется по формуле:
существует и вычисляется по формуле: 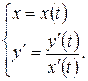
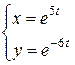 , которую будем мыслить как функцию
, которую будем мыслить как функцию 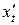 и
и  :
: 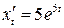 ,
,  .
. .
.
 . Находим
. Находим 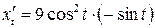 ,
, 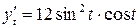 .
. .
.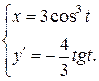
 – вся числовая ось. На интервалах
– вся числовая ось. На интервалах 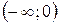 ,
, 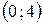 ,
,  функция непрерывна. Разрывы возможны лишь в точках
функция непрерывна. Разрывы возможны лишь в точках  и
и  . Найдем односторонние пределы функции в точке
. Найдем односторонние пределы функции в точке  ,
, .
. , и правосторонний предел
, и правосторонний предел  , но между собой они не равны. Поэтому точка
, но между собой они не равны. Поэтому точка  ,
,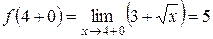 .
. . Так как
. Так как  , то в точке
, то в точке  .
. есть множество
есть множество  . На интервалах
. На интервалах 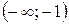 ,
,  функция непрерывна. Поэтому разрыв возможен только в точке
функция непрерывна. Поэтому разрыв возможен только в точке  . Найдем односторонние пределы функции в точке
. Найдем односторонние пределы функции в точке  ,
,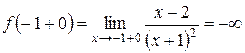 .
.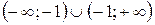 .
. – вся числовая ось кроме точек 1 и –2. Поэтому разрывы возможны только в этих точках.
– вся числовая ось кроме точек 1 и –2. Поэтому разрывы возможны только в этих точках. :
: ,
,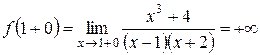 .
. :
: ,
,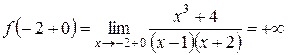 .
. .
.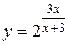 – вся числовая ось, кроме точки –3. На интервалах
– вся числовая ось, кроме точки –3. На интервалах  ,
,  функция непрерывна. Поэтому разрыв возможен только в точке
функция непрерывна. Поэтому разрыв возможен только в точке  . Найдем односторонние пределы функции в точке
. Найдем односторонние пределы функции в точке 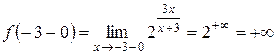 ,
, .
.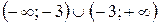 .
. Здесь имеет место неопределенность
Здесь имеет место неопределенность  . Разложим на множители числитель и знаменатель дроби:
. Разложим на множители числитель и знаменатель дроби: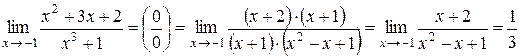 .
. ,
,  .
.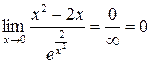 .
. многочлен эквивалентен своему одночлену с наивысшей степенью. По теореме 7 на стр. 18 числитель и знаменатель можно заменить на эквивалентные им функции. Имеем:
многочлен эквивалентен своему одночлену с наивысшей степенью. По теореме 7 на стр. 18 числитель и знаменатель можно заменить на эквивалентные им функции. Имеем: .
. и
и  . Заменяя
. Заменяя  эквивалентной ей функцией
эквивалентной ей функцией 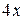 и
и  – функцией
– функцией  , получаем:
, получаем: .
.
 ,
,  . Заменяя числитель и знаменатель эквивалентными им функциями, получаем:
. Заменяя числитель и знаменатель эквивалентными им функциями, получаем: .
. ,
, 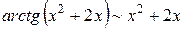 . Получаем:
. Получаем: .
.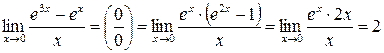 .
.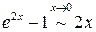 .
. . Получаем:
. Получаем:
 .
.
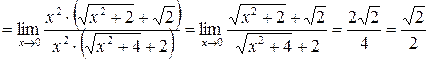 .
. .
.
 .
.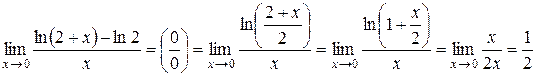 .
.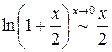 .
.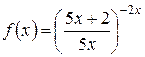 и прологарифмируем данное равенство. Получаем:
и прологарифмируем данное равенство. Получаем:

 (мы применили эквивалентность
(мы применили эквивалентность 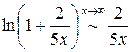 ). Перейдем теперь от логарифма к самой функции:
). Перейдем теперь от логарифма к самой функции: .
. .
. .
. .
.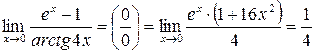 .
. .
. .
.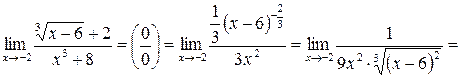
 .
. .
.
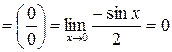 .
. .
.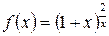 . Имеем:
. Имеем:  . Далее:
. Далее: .
. .
.


