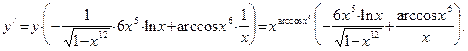В данном разделе мы напомним известные из средней школы факты, связанные с вычислением производной. Все эти утверждения будут доказаны нами после изучения теории пределов. Начнем с формального определения производной.
Пусть функция  определена на открытом интервале
определена на открытом интервале 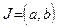 действительной прямой R, точка
действительной прямой R, точка  и число
и число  (называемое приращением независимой переменной x) таково, что
(называемое приращением независимой переменной x) таково, что  . При этом выражение
. При этом выражение  называют приращением данной функции в точке
называют приращением данной функции в точке  .
.
Определение 1. Производной  функции
функции  в точке
в точке  называется предел отношения приращения функции в точке
называется предел отношения приращения функции в точке  к приращению независимой переменной, когда приращение
к приращению независимой переменной, когда приращение  независимой переменной стремится к нулю, то есть
независимой переменной стремится к нулю, то есть
|
|  = =  . .
|
(1)
|
Функция  называется дифференцируемой на интервале
называется дифференцируемой на интервале 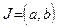 , если она имеет производную в каждой точке этого интервала. Процесс вычисления производной называется дифференцированием.
, если она имеет производную в каждой точке этого интервала. Процесс вычисления производной называется дифференцированием.
Для того, чтобы освоить технику вычисления производной, необходимо знать правила дифференцирования, таблицу производных элементарных функций, а также уметь четко определять порядок действий в математическом выражении.
Правила дифференцирования
1. Производная постоянной функции равна нулю, то есть если  , то
, то
|
|  . .
|
|
2. Производная суммы двух функций равна сумме производных этих функций, то есть если  и
и  существуют, то
существуют, то
|
|  . .
|
|
3. Постоянный множитель можно вынести за знак производной, то есть если  , а
, а  существует, то
существует, то
|
|  . .
|
|
4. Производная произведения двух функций равна производной первой функции, умноженной на вторую, плюс первая функция, умноженная на производную второй; то есть если  и
и  существуют, то
существуют, то
|
|  . .
|
|
5. Производная частного двух функций равна дроби, знаменатель которой равен квадрату знаменателя исходной дроби, а в числителе которой стоит производная числителя исходной дроби, умноженная на ее знаменатель, минус числитель исходной дроби, умноженный на производную ее знаменателя; то есть если  и
и  существуют и
существуют и  , то
, то
|
|  . .
|
|
6. Производная сложной функции (цепное правило): если  , где в свою очередь
, где в свою очередь  , и если
, и если  и
и  существуют, то
существуют, то
|
|  . .
|
|
Таблица производных элементарных функций
| Производные степенной, показательной и логарифмической функций
| Производные тригонометрических функций
| Производные обратных тригонометрических функций
|
 (где (где 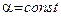 ) )
| 
| 
|
 (где (где  ) )
| 
| 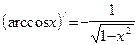
|
 (где (где  , ,  ) )
| 
|  
|
 (частные случаи предыдущих двух формул при (частные случаи предыдущих двух формул при  , где e – натуральное число) , где e – натуральное число)
|

|
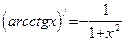
|
Порядок действий в математическом выражении
и дифференцирование сложных функций
Рассмотрим две функции:  и
и  . Эти функции очень похожи. Для правильного их дифференцирования нужно отчетливо выделить операции, которые производятся над переменной x в данных математических выражениях. У первой функции переменная x сначала возводится в куб, а затем на полученный результат действует функция синус. Таким образом,
. Эти функции очень похожи. Для правильного их дифференцирования нужно отчетливо выделить операции, которые производятся над переменной x в данных математических выражениях. У первой функции переменная x сначала возводится в куб, а затем на полученный результат действует функция синус. Таким образом,  . Наоборот, у второй функции переменная x сначала подвергается действию функции синус, а затем результат возводится в куб, то есть
. Наоборот, у второй функции переменная x сначала подвергается действию функции синус, а затем результат возводится в куб, то есть 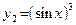 . Найдем производные этих функций, применяя цепное правило и таблицу производных. Заметим, что начинать дифференцирование нужно с последней операции, затем дифференцируют предпоследнюю операцию и, действуя таким образом, заканчивают производной первой операции.
. Найдем производные этих функций, применяя цепное правило и таблицу производных. Заметим, что начинать дифференцирование нужно с последней операции, затем дифференцируют предпоследнюю операцию и, действуя таким образом, заканчивают производной первой операции.
Последней операцией функции  является операция синус, производная которой есть косинус, поэтому первым звеном цепного правила является функция
является операция синус, производная которой есть косинус, поэтому первым звеном цепного правила является функция  . При этом у полученной нами функции сохранился аргумент, которым обладал синус. Предпоследней операцией у рассматриваемой функции является возведение в куб (эта операция в данном примере одновременно является первой). Поэтому второе (и заключительное) звено цепного правила будет производная степенной функции
. При этом у полученной нами функции сохранился аргумент, которым обладал синус. Предпоследней операцией у рассматриваемой функции является возведение в куб (эта операция в данном примере одновременно является первой). Поэтому второе (и заключительное) звено цепного правила будет производная степенной функции 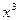 , то есть функция
, то есть функция  . Руководствуясь формулой 6 правил дифференцирования, окончательно получаем:
. Руководствуясь формулой 6 правил дифференцирования, окончательно получаем:  .
.
Последней операцией функции 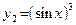 является возведение в куб, поэтому у ее производной первым звеном будет функция
является возведение в куб, поэтому у ее производной первым звеном будет функция 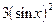 . Отметим, что так как у исходной функции аргументом, который возводился в куб, был
. Отметим, что так как у исходной функции аргументом, который возводился в куб, был  , то этот аргумент сохранился и в первом звене дифференцирования. Предпоследней (и одновременно первой) операцией рассматриваемой функции является синус, поэтому второе звено будет равно
, то этот аргумент сохранился и в первом звене дифференцирования. Предпоследней (и одновременно первой) операцией рассматриваемой функции является синус, поэтому второе звено будет равно  . Окончательно получаем:
. Окончательно получаем:  .
.
Продифференцируем теперь сложную функцию, состоящую из трех операций, а именно функцию  . Вычленим составляющие эту функцию простые операции:
. Вычленим составляющие эту функцию простые операции:  . Здесь первая операция – возведение переменной x в пятую степень, вторая операция – взятие тангенса от полученного результата и, наконец, последняя операция – возведение всего, что получилось, в квадрат. При дифференцировании цепное правило даст три звена. Первое звено получим, дифференцируя последнюю операцию. Оно будет состоять из функции
. Здесь первая операция – возведение переменной x в пятую степень, вторая операция – взятие тангенса от полученного результата и, наконец, последняя операция – возведение всего, что получилось, в квадрат. При дифференцировании цепное правило даст три звена. Первое звено получим, дифференцируя последнюю операцию. Оно будет состоять из функции  . Второе звено – производная предпоследней операции – равно
. Второе звено – производная предпоследней операции – равно  . И, наконец, последнее звено есть функция
. И, наконец, последнее звено есть функция  . В результате имеем:
. В результате имеем:  .
.
Вычислим производную еще более сложной функции  . Здесь первой операцией целесообразно считать многочлен
. Здесь первой операцией целесообразно считать многочлен  . Вторая операция – это взятие арктангенса от многочлена, третья операция – вычисление натурального логарифма, четвертая операция – возведение всего полученного в седьмую степень. Применяя цепное правило, получаем:
. Вторая операция – это взятие арктангенса от многочлена, третья операция – вычисление натурального логарифма, четвертая операция – возведение всего полученного в седьмую степень. Применяя цепное правило, получаем:  .
.
Некоторые замечания, полезные при дифференцировании
1. Если нужно продифференцировать функцию, содержащую радикалы, то перед дифференцированием эти радикалы следует перевести в дробные степени. Например, пусть  . Сначала преобразовываем эту функцию к виду:
. Сначала преобразовываем эту функцию к виду:  . Теперь производная вычисляется без труда:
. Теперь производная вычисляется без труда: 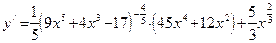 .
.
2. Если нужно продифференцировать дробь, числитель которой – постоянное число, то перед дифференцированием знаменатель с показателем минус единица нужно поместить в числитель. Пусть, например,  . Преобразовываем функцию следующим образом:
. Преобразовываем функцию следующим образом:  . Теперь
. Теперь 
 .
.
3. При дифференцировании не следует путать производные степенной и показательной функций. Для примера рассмотрим функции  и
и 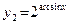 . У функции
. У функции  первая операция есть функция арксинус, а вторая операция – степенная функция (возведение в степень с постоянным показателем 2). Поэтому, следуя правилу дифференцирования сложной функции, получим
первая операция есть функция арксинус, а вторая операция – степенная функция (возведение в степень с постоянным показателем 2). Поэтому, следуя правилу дифференцирования сложной функции, получим  . У второй функции первая операция также есть функция арксинус, но вторая операция – это взятие постоянного числа 2 с показателем
. У второй функции первая операция также есть функция арксинус, но вторая операция – это взятие постоянного числа 2 с показателем  , то есть показательная функция. Поэтому
, то есть показательная функция. Поэтому  .
.
4. Если нужно продифференцировать логарифмическую функцию, внутри которой содержится степень, то, применяя свойства логарифма, показатель степени следует вынести за знак логарифма. Пусть, например,  . Заменив радикал дробной степенью и вынеся показатель за знак логарифма, получим:
. Заменив радикал дробной степенью и вынеся показатель за знак логарифма, получим:  Поэтому
Поэтому  .
.
5. Если внутрь какой-либо функции вставлено произведение или частное двух функций, то в этом случае не следует пытаться одним махом вычислить производную данной сложной функции, а лучше действовать поэтапно. Например, если  , то ее производную следует вычислять следующим образом:
, то ее производную следует вычислять следующим образом: 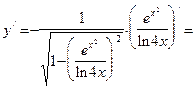
 .
.
Логарифмическое дифференцирование
Рассмотрим метод нахождения производной степенно-показательной функции  , у которой переменная x находится как в основании степени, так и в показателе. Прологарифмируем данную функцию:
, у которой переменная x находится как в основании степени, так и в показателе. Прологарифмируем данную функцию:  . Теперь продифференцируем обе части полученного равенства:
. Теперь продифференцируем обе части полученного равенства:  . Отсюда
. Отсюда 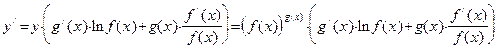 .
.
Пример 1. Найдем производную функции 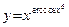 . Применим метод логарифмического дифференцирования. Прологарифмируем данную функцию:
. Применим метод логарифмического дифференцирования. Прологарифмируем данную функцию:  . Теперь найдем производные обеих частей полученного равенства:
. Теперь найдем производные обеих частей полученного равенства:  . В результате получаем:
. В результате получаем: 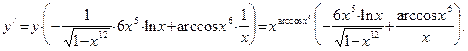

 определена на открытом интервале
определена на открытом интервале 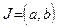 действительной прямой R, точка
действительной прямой R, точка  и число
и число  (называемое приращением независимой переменной x) таково, что
(называемое приращением независимой переменной x) таково, что  . При этом выражение
. При этом выражение  называют приращением данной функции в точке
называют приращением данной функции в точке  функции
функции  .
.
 , то
, то .
.
 и
и  существуют, то
существуют, то .
.
 , а
, а  .
.
 .
.
 , то
, то .
.
 , где в свою очередь
, где в свою очередь  , и если
, и если  существуют, то
существуют, то .
.
 (где
(где 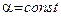 )
)


 (где
(где  )
)

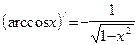
 (где
(где  )
)



 (частные случаи предыдущих двух формул при
(частные случаи предыдущих двух формул при  , где e – натуральное число)
, где e – натуральное число)

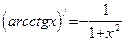
 и
и  . Эти функции очень похожи. Для правильного их дифференцирования нужно отчетливо выделить операции, которые производятся над переменной x в данных математических выражениях. У первой функции переменная x сначала возводится в куб, а затем на полученный результат действует функция синус. Таким образом,
. Эти функции очень похожи. Для правильного их дифференцирования нужно отчетливо выделить операции, которые производятся над переменной x в данных математических выражениях. У первой функции переменная x сначала возводится в куб, а затем на полученный результат действует функция синус. Таким образом,  . Наоборот, у второй функции переменная x сначала подвергается действию функции синус, а затем результат возводится в куб, то есть
. Наоборот, у второй функции переменная x сначала подвергается действию функции синус, а затем результат возводится в куб, то есть 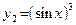 . Найдем производные этих функций, применяя цепное правило и таблицу производных. Заметим, что начинать дифференцирование нужно с последней операции, затем дифференцируют предпоследнюю операцию и, действуя таким образом, заканчивают производной первой операции.
. Найдем производные этих функций, применяя цепное правило и таблицу производных. Заметим, что начинать дифференцирование нужно с последней операции, затем дифференцируют предпоследнюю операцию и, действуя таким образом, заканчивают производной первой операции. . При этом у полученной нами функции сохранился аргумент, которым обладал синус. Предпоследней операцией у рассматриваемой функции является возведение в куб (эта операция в данном примере одновременно является первой). Поэтому второе (и заключительное) звено цепного правила будет производная степенной функции
. При этом у полученной нами функции сохранился аргумент, которым обладал синус. Предпоследней операцией у рассматриваемой функции является возведение в куб (эта операция в данном примере одновременно является первой). Поэтому второе (и заключительное) звено цепного правила будет производная степенной функции 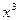 , то есть функция
, то есть функция  . Руководствуясь формулой 6 правил дифференцирования, окончательно получаем:
. Руководствуясь формулой 6 правил дифференцирования, окончательно получаем:  .
.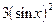 . Отметим, что так как у исходной функции аргументом, который возводился в куб, был
. Отметим, что так как у исходной функции аргументом, который возводился в куб, был  , то этот аргумент сохранился и в первом звене дифференцирования. Предпоследней (и одновременно первой) операцией рассматриваемой функции является синус, поэтому второе звено будет равно
, то этот аргумент сохранился и в первом звене дифференцирования. Предпоследней (и одновременно первой) операцией рассматриваемой функции является синус, поэтому второе звено будет равно  . Окончательно получаем:
. Окончательно получаем:  .
. . Вычленим составляющие эту функцию простые операции:
. Вычленим составляющие эту функцию простые операции:  . Здесь первая операция – возведение переменной x в пятую степень, вторая операция – взятие тангенса от полученного результата и, наконец, последняя операция – возведение всего, что получилось, в квадрат. При дифференцировании цепное правило даст три звена. Первое звено получим, дифференцируя последнюю операцию. Оно будет состоять из функции
. Здесь первая операция – возведение переменной x в пятую степень, вторая операция – взятие тангенса от полученного результата и, наконец, последняя операция – возведение всего, что получилось, в квадрат. При дифференцировании цепное правило даст три звена. Первое звено получим, дифференцируя последнюю операцию. Оно будет состоять из функции  . Второе звено – производная предпоследней операции – равно
. Второе звено – производная предпоследней операции – равно  . И, наконец, последнее звено есть функция
. И, наконец, последнее звено есть функция  . В результате имеем:
. В результате имеем:  .
. . Здесь первой операцией целесообразно считать многочлен
. Здесь первой операцией целесообразно считать многочлен  . Вторая операция – это взятие арктангенса от многочлена, третья операция – вычисление натурального логарифма, четвертая операция – возведение всего полученного в седьмую степень. Применяя цепное правило, получаем:
. Вторая операция – это взятие арктангенса от многочлена, третья операция – вычисление натурального логарифма, четвертая операция – возведение всего полученного в седьмую степень. Применяя цепное правило, получаем:  .
. . Сначала преобразовываем эту функцию к виду:
. Сначала преобразовываем эту функцию к виду:  . Теперь производная вычисляется без труда:
. Теперь производная вычисляется без труда: 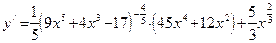 .
. . Преобразовываем функцию следующим образом:
. Преобразовываем функцию следующим образом:  . Теперь
. Теперь 
 .
. и
и 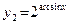 . У функции
. У функции  первая операция есть функция арксинус, а вторая операция – степенная функция (возведение в степень с постоянным показателем 2). Поэтому, следуя правилу дифференцирования сложной функции, получим
первая операция есть функция арксинус, а вторая операция – степенная функция (возведение в степень с постоянным показателем 2). Поэтому, следуя правилу дифференцирования сложной функции, получим  . У второй функции первая операция также есть функция арксинус, но вторая операция – это взятие постоянного числа 2 с показателем
. У второй функции первая операция также есть функция арксинус, но вторая операция – это взятие постоянного числа 2 с показателем  , то есть показательная функция. Поэтому
, то есть показательная функция. Поэтому  .
. . Заменив радикал дробной степенью и вынеся показатель за знак логарифма, получим:
. Заменив радикал дробной степенью и вынеся показатель за знак логарифма, получим:  Поэтому
Поэтому  .
. , то ее производную следует вычислять следующим образом:
, то ее производную следует вычислять следующим образом: 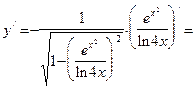
 .
. , у которой переменная x находится как в основании степени, так и в показателе. Прологарифмируем данную функцию:
, у которой переменная x находится как в основании степени, так и в показателе. Прологарифмируем данную функцию:  . Теперь продифференцируем обе части полученного равенства:
. Теперь продифференцируем обе части полученного равенства:  . Отсюда
. Отсюда 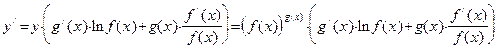 .
.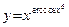 . Применим метод логарифмического дифференцирования. Прологарифмируем данную функцию:
. Применим метод логарифмического дифференцирования. Прологарифмируем данную функцию:  . Теперь найдем производные обеих частей полученного равенства:
. Теперь найдем производные обеих частей полученного равенства:  . В результате получаем:
. В результате получаем: