Техника вычисления пределов
В данной лекции мы, в основном, будем иметь дело с пределами от элементарных функций. Используя теорему 4, легко вычислить предел такой функции, когда точка, к которой стремится аргумент, принадлежит области определения функции. Рассмотрим соответствующий пример.
Пример 9. Вычислить предел:  . Так как в точке
. Так как в точке 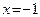 знаменатель функции, стоящей под знаком предела, неравен нулю, то эта функция непрерывна в точке
знаменатель функции, стоящей под знаком предела, неравен нулю, то эта функция непрерывна в точке 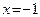 . Следуя определению 9, для подсчета b достаточно вычислить эту функцию при
. Следуя определению 9, для подсчета b достаточно вычислить эту функцию при 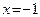 , то есть
, то есть  . €
. €
Наша основная задача – научится вычислять пределы, когда точка, к которой стремится аргумент, не принадлежит области определения функции, но " примыкает" к области определения.
Пример 10. Вычислить предел:  . Очевидно, точка
. Очевидно, точка  не принадлежит области определения функции, стоящей под знаком предела, поэтому определение 9 неприменимо. Однако, первый сомножитель функции, стоящей под знаком предела, ограничен при
не принадлежит области определения функции, стоящей под знаком предела, поэтому определение 9 неприменимо. Однако, первый сомножитель функции, стоящей под знаком предела, ограничен при  , так как
, так как
|
| 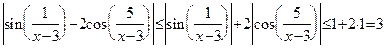 , ,
|
|
а второй сомножитель – б.м.ф. при 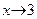 , так как
, так как  . По свойству 8 предела функции
. По свойству 8 предела функции 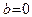 . €
. €
Следующая теорема аккумулирует предельные соотношения, хорошо известные из школьного курса математики.
Теорема 8. 1) Если  , то
, то  ,
,  ; если же
; если же  , то
, то  , а
, а  .
.
2) Если  , то
, то  ,
,  ; если же
; если же  , то
, то 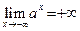 , а
, а 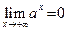 . В частности,
. В частности,  ,
,  .
.
3) Если  , то
, то  ,
,  ; если же
; если же  , то
, то  , а
, а  . В частности,
. В частности,  ,
,  .
.
4)  .
.
5)  .
.
6)  . €
. €
Читателю рекомендуется просмотреть все эти равенства на графиках функций.
Запишем некоторые соотношения, связанные с символом 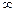 . Принимая во внимание лемму 2, можно записать:
. Принимая во внимание лемму 2, можно записать:
|
|  . .
|
(11)
|
Легко также обосновать следующие соотношения (здесь c – ненулевая константа):
|
| 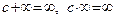 , ,  . .
|
(12)
|
Неопределенностями будем называть выражения вида:
|
| 
|
(13)
|
и т.д. Соотношения типа (11) и (12), а также неопределенности типа (13) нетрудно записать и для символов  .
.
Пример 11. Вычислим предел  . Применив эквивалентность (9) и теорему 7, получаем:
. Применив эквивалентность (9) и теорему 7, получаем:  . Последнее равенство взято из (12).
. Последнее равенство взято из (12).
Пример 12. Вычислим предел 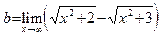 . Переходя к пределу в каждом из радикалов, получаем неопределенность вида
. Переходя к пределу в каждом из радикалов, получаем неопределенность вида  . Разделив и умножив выражение, стоящее под знаком предела, на сопряженное выражение
. Разделив и умножив выражение, стоящее под знаком предела, на сопряженное выражение  , имеем:
, имеем:
 .
.
Пример 13. Вычислим предел  . Подставив
. Подставив  отдельно в числитель и знаменатель, убеждаемся, что получили неопределенность вида
отдельно в числитель и знаменатель, убеждаемся, что получили неопределенность вида  . Так как при
. Так как при  имеем
имеем 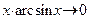 , то для числителя верна цепочка эквивалентностей при
, то для числителя верна цепочка эквивалентностей при  :
:
Аналогично, для знаменателя получаем:
По теореме 7 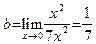 .
.
Правило Лопиталя
Сейчас мы покажем, как можно вычислять пределы, используя понятие производной (см. вводную лекцию).
Теорема 9 (правило Лопиталя). Пусть функции  и
и  определены и дифференцируемы в некоторой окрестности точки a (за исключением, быть может, самой точки a) и в этой окрестности
определены и дифференцируемы в некоторой окрестности точки a (за исключением, быть может, самой точки a) и в этой окрестности  Предположим, что:
Предположим, что:
1) 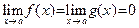 (то есть при
(то есть при  дробь
дробь  превращается в неопределенность типа
превращается в неопределенность типа  );
);
2) 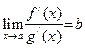 (где b – действительное число либо одна из точек:
(где b – действительное число либо одна из точек:  или
или 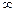 ).
).
Тогда 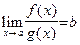 .
.
Теорема остается справедливой, если вместо условия 1) потребовать выполнение следующего условия:

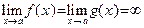 (то есть при
(то есть при  дробь
дробь  превращается в неопределенность типа
превращается в неопределенность типа  ).
).
Мы дадим доказательство этой теоремы после более глубокого изучения понятия производной.
Заметим, что теорема 9 остается справедливой, если в ее формулировке вместо символа  везде писать
везде писать  или
или 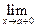 . В частности, данная теорема справедлива, когда
. В частности, данная теорема справедлива, когда  или
или  .
.
Пример 14. Вычислим предел 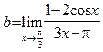 . Очевидно, здесь мы имеем неопределенность типа
. Очевидно, здесь мы имеем неопределенность типа  . Применяем правило Лопиталя:
. Применяем правило Лопиталя:
|
| 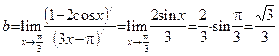 . .
|
|
|
| €
|
| | | | |
Пример 15. Вычислим предел  . В силу непрерывности логарифмической функции, пункта 2) леммы 1 и пункта 6) теоремы 8 получаем, что предел второго сомножителя равен
. В силу непрерывности логарифмической функции, пункта 2) леммы 1 и пункта 6) теоремы 8 получаем, что предел второго сомножителя равен 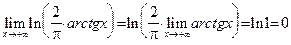 . То есть в данном случае мы получаем неопределенность типа
. То есть в данном случае мы получаем неопределенность типа 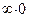 . Преобразуем ее к неопределенности типа
. Преобразуем ее к неопределенности типа  и применим правило Лопиталя:
и применим правило Лопиталя:
|
|   . .
|
|
|
| €
| |
| | | | | |
При решении предыдущего примера мы использовали не только правило Лопиталя, но, заменив в знаменателе 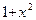 на
на 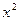 , применили эквивалентность (9). На самом деле, при вычислении многих пределов применение правила Лопиталя часто комбинируется с применением эквивалентностей.
, применили эквивалентность (9). На самом деле, при вычислении многих пределов применение правила Лопиталя часто комбинируется с применением эквивалентностей.
Пример 16. Имеем:
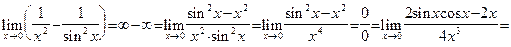

 .
.
Пример 17. 1) Докажем, что если  , то
, то
|
|  . .
|
(14)
|
Применяя теорему 8 и правило Лопиталя, имеем: 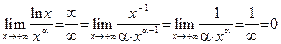 .
.
2) Докажем, что если  и
и  , то
, то
|
|  . .
|
(15)
|
Имеем: 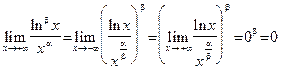 .
.
Пример 18. Докажем, что при 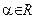
|
|  . .
|
(16)
|
При  равенство (16) очевидно. Пусть
равенство (16) очевидно. Пусть  . Пусть n – наименьшее натуральное число, удовлетворяющее неравенству
. Пусть n – наименьшее натуральное число, удовлетворяющее неравенству  . Применяя n раз правило Лопиталя, получим:
. Применяя n раз правило Лопиталя, получим:
 .
.
Определение 13. Будем говорить, что функция  " много меньше" функции
" много меньше" функции  при
при  (обозначается
(обозначается  при
при  ), если
), если 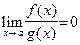 .
.
Из равенств (14) и (16) следует, что если  , то при
, то при 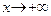
 .
.
Теорема 10. Если при 
 , то
, то  ~
~ 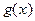 при
при  .
.
Доказательство тривиально.
Пример 19. Вычислим предел  . Имеем:
. Имеем:  . По правилу Лопиталя
. По правилу Лопиталя  (в предпоследнем равенстве была применена теорема 10 и замечание перед ней). Окончательно:
(в предпоследнем равенстве была применена теорема 10 и замечание перед ней). Окончательно: 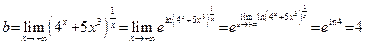 . €
. €

 . Так как в точке
. Так как в точке 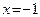 знаменатель функции, стоящей под знаком предела, неравен нулю, то эта функция непрерывна в точке
знаменатель функции, стоящей под знаком предела, неравен нулю, то эта функция непрерывна в точке  . €
. € . Очевидно, точка
. Очевидно, точка  не принадлежит области определения функции, стоящей под знаком предела, поэтому определение 9 неприменимо. Однако, первый сомножитель функции, стоящей под знаком предела, ограничен при
не принадлежит области определения функции, стоящей под знаком предела, поэтому определение 9 неприменимо. Однако, первый сомножитель функции, стоящей под знаком предела, ограничен при  , так как
, так как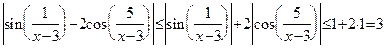 ,
,
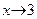 , так как
, так как  . По свойству 8 предела функции
. По свойству 8 предела функции 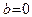 . €
. € , то
, то  ,
,  ; если же
; если же  , то
, то  , а
, а  .
. , то
, то  ,
,  ; если же
; если же  , то
, то 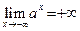 , а
, а 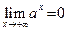 . В частности,
. В частности,  ,
,  .
. ,
,  ; если же
; если же  , а
, а  . В частности,
. В частности,  ,
,  .
. .
. .
. . €
. €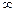 . Принимая во внимание лемму 2, можно записать:
. Принимая во внимание лемму 2, можно записать: .
.
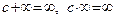 ,
,  .
.

 .
. . Применив эквивалентность (9) и теорему 7, получаем:
. Применив эквивалентность (9) и теорему 7, получаем:  . Последнее равенство взято из (12).
. Последнее равенство взято из (12).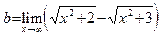 . Переходя к пределу в каждом из радикалов, получаем неопределенность вида
. Переходя к пределу в каждом из радикалов, получаем неопределенность вида  . Разделив и умножив выражение, стоящее под знаком предела, на сопряженное выражение
. Разделив и умножив выражение, стоящее под знаком предела, на сопряженное выражение  , имеем:
, имеем: .
. . Подставив
. Подставив  отдельно в числитель и знаменатель, убеждаемся, что получили неопределенность вида
отдельно в числитель и знаменатель, убеждаемся, что получили неопределенность вида  . Так как при
. Так как при  имеем
имеем 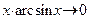 , то для числителя верна цепочка эквивалентностей при
, то для числителя верна цепочка эквивалентностей при  ~
~  ~
~ 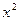 .
.
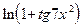 ~
~  ~
~  .
.
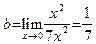 .
. и
и  определены и дифференцируемы в некоторой окрестности точки a (за исключением, быть может, самой точки a) и в этой окрестности
определены и дифференцируемы в некоторой окрестности точки a (за исключением, быть может, самой точки a) и в этой окрестности  Предположим, что:
Предположим, что: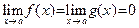 (то есть при
(то есть при  дробь
дробь  превращается в неопределенность типа
превращается в неопределенность типа 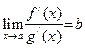 (где b – действительное число либо одна из точек:
(где b – действительное число либо одна из точек:  или
или 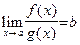 .
.
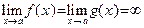 (то есть при
(то есть при  ).
). везде писать
везде писать  или
или 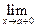 . В частности, данная теорема справедлива, когда
. В частности, данная теорема справедлива, когда  или
или  .
.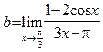 . Очевидно, здесь мы имеем неопределенность типа
. Очевидно, здесь мы имеем неопределенность типа 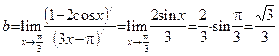 .
.
 . В силу непрерывности логарифмической функции, пункта 2) леммы 1 и пункта 6) теоремы 8 получаем, что предел второго сомножителя равен
. В силу непрерывности логарифмической функции, пункта 2) леммы 1 и пункта 6) теоремы 8 получаем, что предел второго сомножителя равен 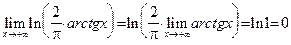 . То есть в данном случае мы получаем неопределенность типа
. То есть в данном случае мы получаем неопределенность типа 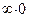 . Преобразуем ее к неопределенности типа
. Преобразуем ее к неопределенности типа 
 .
.
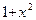 на
на 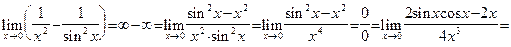

 .
. .
.
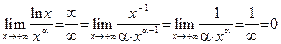 .
. , то
, то .
.
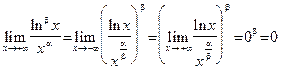 .
.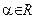
 .
.
 равенство (16) очевидно. Пусть
равенство (16) очевидно. Пусть  . Применяя n раз правило Лопиталя, получим:
. Применяя n раз правило Лопиталя, получим: .
. при
при 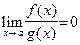 .
.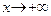
 .
. ~
~ 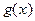 при
при  . Имеем:
. Имеем:  . По правилу Лопиталя
. По правилу Лопиталя  (в предпоследнем равенстве была применена теорема 10 и замечание перед ней). Окончательно:
(в предпоследнем равенстве была применена теорема 10 и замечание перед ней). Окончательно: 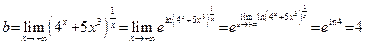 . €
. €


