Лекция 4. Определение 9. Функция называется непрерывной в точке D(y), если
Непрерывные функции
Определение 9. Функция
Если равенство (5) не выполняется, то функция В примерах 4 и 5 рассматриваемые функции не были определены в точке Пример 7. Рассмотрим функцию из примера 5, но " доопределенную" в точке
График этой функции имеет вид:
Согласно определению 8, вычисляя предел функции при
Пример 8. Изменим значение функции из примера 7 только в одной точке, положив
Переопределением функции в точке
Определение 10. Функция
Легко видеть, что в примерах 4–7 исследуемые функции непрерывны всюду на числовой прямой за исключением точки Следующая лемма будет полезна при доказательстве свойств непрерывных функций. Лемма 1. 1) Пусть 2) Если Доказательство этой леммы почти очевидно и предоставляется читателю.
Свойства непрерывных функций
1. Постоянная функция непрерывна. 2. Сумма двух непрерывных функций непрерывна. 3. Произведение непрерывной функции на число есть непрерывная функция. 4. Произведение двух непрерывных функций непрерывно. 5. Частное двух непрерывных функций непрерывно в точках, в которых знаменатель неравен нулю. 6. Сложная функция, состоящая из двух непрерывных функций, непрерывна (определение сложной функции содержится в вводной лекции в шестом правиле дифференцирования). Доказательство. Доказательство свойств 1–5 непосредственно следуют из соответствующих свойств предела функции. Докажем свойство 6. Пусть функция
Теорема 3. Основные элементарные функции (то есть функции, представленные в таблице производных из вводной лекции) непрерывны на своих областях определения. Доказательство. Докажем теорему только для тригонометрических функций. Во-первых, используя первый замечательный предел, получаем:
Далее, по известной формуле: Для доказательства непрерывности функции Непрерывность функций
Теорема 4. Все элементарные функции (то есть те функции, которые образованы из основных элементарных функций с помощью конечного числа арифметических операций и взятия сложных функций) непрерывны на своих областях определения. Доказательство немедленно следует из теоремы 4 и свойств непрерывных функций.
Эквивалентные функции. Бесконечно малые функции (б.м.ф.) и бесконечно большие функции (б.б.ф.).
В последующей части данной лекции мы предполагаем, что a – либо действительное число, либо одна из бесконечно удаленных точек: Определение 11. Функции
Обозначение эквивалентности функций таково: Аналогично определяются и обозначаются эквивалентные функции при
Заметим, что в силу свойства 5 предела функции, равенство (7) равносильно равенству Определение 12. Функция
Легко видеть, что бесконечно малая функция может быть эквивалентна только бесконечно малой функции, а бесконечно большая функция – только бесконечно большой. Теорема 5. При
Доказательство. Первая эквивалентность – это просто первый замечательный предел. Вторая эквивалентность следует из первой и из непрерывности косинуса:
Докажем третью эквивалентность. Представим
Четвертая эквивалентность доказывается так же, как третья. Докажем пятую эквивалентность. Имеем:
Здесь были применены свойство логарифмов, второй замечательный предел и пункт 2) леммы 1, который следует из непрерывности логарифма. Для доказательства последней эквивалентности применим представление:
Связь между б.м.ф. и б.б.ф. устанавливает следующая Лемма 2. Если при Доказательство предоставляется читателю. € Теорема 6. При
где Доказательство. Имеем:
Последние предельные соотношения следуют из леммы 2.
При вычислении пределов с помощью эквивалентных функций весьма полезна следующая простая Теорема 7. Если при
в случае, когда один из этих пределов существует. Доказательство. Имеем:
Заметим, однако, что если даже внутрь одной функции засунуть две эквивалентные функции, то полученные функции, вообще говоря, будут неэквивалентными. Например, по теореме 6 при
То есть при
|

 называется непрерывной в точке
называется непрерывной в точке  D(y), если
D(y), если .
.
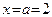 , поэтому не имеет смысла говорить о непрерывности этих функций в данной точке.
, поэтому не имеет смысла говорить о непрерывности этих функций в данной точке. .
.

 мы не используем значение функции в точке a. Поэтому предел, вычисленный нами в примере 5, сохраняет свое значение, то есть и в данном случае
мы не используем значение функции в точке a. Поэтому предел, вычисленный нами в примере 5, сохраняет свое значение, то есть и в данном случае  . Значение же функции в точке
. Значение же функции в точке  . Равенство (5) не выполняется, поэтому данная функция разрывна в точке
. Равенство (5) не выполняется, поэтому данная функция разрывна в точке  . График полученной функции имеет вид:
. График полученной функции имеет вид:
 . Равенство (5) имеет место, то есть данная функция непрерывна в точке
. Равенство (5) имеет место, то есть данная функция непрерывна в точке 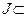 D(y), если она непрерывна в каждой точке этого множества.
D(y), если она непрерывна в каждой точке этого множества. , функция
, функция  строго монотонно возрастает (или строго монотонно убывает) в тех точках окрестности a, в которых она определена, а функция
строго монотонно возрастает (или строго монотонно убывает) в тех точках окрестности a, в которых она определена, а функция  имеет предел при
имеет предел при 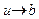 .Тогда
.Тогда  .
. , то
, то  .
. (то есть
(то есть  . По пункту 2) леммы 1 имеем:
. По пункту 2) леммы 1 имеем:  , то есть функция
, то есть функция  непрерывна в точке
непрерывна в точке 
 . Так как
. Так как  , а по предыдущему замечанию и свойству 6 непрерывных функций
, а по предыдущему замечанию и свойству 6 непрерывных функций  , то по свойству 8 предела функции имеем:
, то по свойству 8 предела функции имеем:  . Отсюда немедленно следует соотношение
. Отсюда немедленно следует соотношение  , которое и доказывает непрерывность функции
, которое и доказывает непрерывность функции  при любом действительном a.
при любом действительном a. достаточно применить формулу приведения
достаточно применить формулу приведения  , непрерывность синуса и свойство 6 непрерывных функций.
, непрерывность синуса и свойство 6 непрерывных функций. и
и 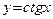 (на своих областях определения) следует из непрерывности синуса и косинуса и свойства 5 непрерывных функций.
(на своих областях определения) следует из непрерывности синуса и косинуса и свойства 5 непрерывных функций.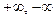 или просто
или просто 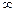 .
. называются эквивалентными при
называются эквивалентными при  , если
, если .
.
 ~
~  при
при  и
и  .
. .
. . Функция
. Функция  .
. справедлива следующая цепочка эквивалентных б.м.ф.:
справедлива следующая цепочка эквивалентных б.м.ф.: ~
~  ~
~  ~
~  ~
~  ~
~ 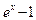
 .
.
 , где
, где  , а
, а  – строго монотонно возрастающая функция. Используя пункт 1) леммы 1, а также равенство
– строго монотонно возрастающая функция. Используя пункт 1) леммы 1, а также равенство  , следующее из непрерывности функции арксинус, получаем:
, следующее из непрерывности функции арксинус, получаем: .
.
 .
.
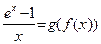 , где
, где  , а
, а  – строго монотонно возрастающая функция. Используя пункт 1) леммы 1, а также равенство
– строго монотонно возрастающая функция. Используя пункт 1) леммы 1, а также равенство  , следующее из непрерывности показательной функции, получаем:
, следующее из непрерывности показательной функции, получаем: .
.
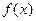 – б.б.ф., то
– б.б.ф., то  – б.м.ф. Наоборот, если при
– б.м.ф. Наоборот, если при  справедлива следующая эквивалентность многочлена своей старшей степени:
справедлива следующая эквивалентность многочлена своей старшей степени: ~
~  ,
,
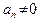 .
.
 .
.
 ~
~ 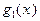 и
и  ~
~ 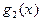 , то
, то
 .
. ~
~ 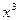 . Подставив эти функции внутрь функции
. Подставив эти функции внутрь функции  , получим функции
, получим функции  и
и  . Имеем:
. Имеем: .
.



