Лекция 6. Эта лекция будет посвящена доказательству правил дифференцирования и формул из таблицы производных элементарных функций (см
Эта лекция будет посвящена доказательству правил дифференцирования и формул из таблицы производных элементарных функций (см. вводную лекцию по технике дифференцирования).
Доказательства правил дифференцирования
Доказательство правила 1. Если
Доказательство правила 2. Действуем по определению 1:
Доказательство правила 3. Имеем:
Лемма 3. Дифференцируемая функция непрерывна; то есть (в обозначениях определения 1), если Доказательство. Применяя свойство 4 предела функции, имеем:
Так как здесь
Доказательство правила 4. Применяя определение производной к функции
Пределы дробей в последней строке равны, соответственно,
Доказательство правила 5. Сначала рассмотрим случай, когда числитель тождественно равен единице. Имеем:
Равенство Применяя 4-е правило дифференцирования к произвольной дроби, получаем:
Доказательство правила 6. Пусть x – фиксировано и
Ввиду произвольности последовательности
Вывод производных степенной, показательной и логарифмической функций
Докажем сначала формулу
Так как x – положительная константа, то
Теперь легко получается формула для произвольной логарифмической функции:
Выведем производную степенной функции. Применим так называемый метод логарифмического дифференцирования. Так как
Тот же метод применим для вывода производной показательной функции:
Вывод производных тригонометрических функций
Покажем, что
В процессе вычислений мы применили эквивалентность Теперь, применяя формулы приведения и цепное правило, получаем:
Далее:
Аналогично выводится производная котангенса.
Вывод производных обратных тригонометрических функций
Лемма 4. Пусть непрерывная функция
Доказательство. Пусть
Ввиду произвольности последовательности
Выведем теперь формулу для производной арксинуса. Положим
Из хорошо известной формулы
Выведем формулу для производной арктангенса. Положим
Опять из известной формулы
|

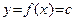 при всех x, то
при всех x, то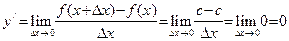 .
.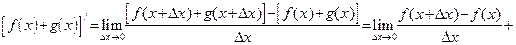
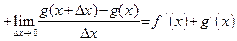 .
.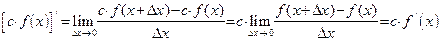 .
. существует, то
существует, то 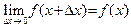 .
.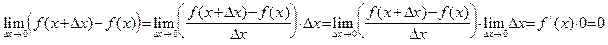 .
.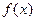 – константа, то из свойств 1–3 предела функции легко выводим требуемое.
– константа, то из свойств 1–3 предела функции легко выводим требуемое. , получаем:
, получаем:


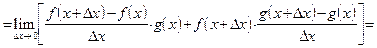
 .
. и
и  . Так как
. Так как  – константа, то
– константа, то 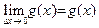 . А по лемме 3 получаем, что
. А по лемме 3 получаем, что 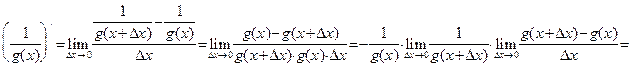
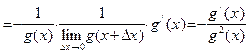 .
. явилось следствием леммы 3.
явилось следствием леммы 3.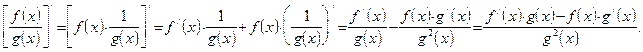
 – произвольная последовательность, строго стремящаяся к x. Обозначим
– произвольная последовательность, строго стремящаяся к x. Обозначим 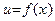 и
и  . Из леммы 3 следует, что
. Из леммы 3 следует, что 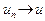 при
при 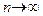 , однако, вообще говоря, эта сходимость может быть и нестрогой (приведите соответствующий пример!). Обозначим через
, однако, вообще говоря, эта сходимость может быть и нестрогой (приведите соответствующий пример!). Обозначим через 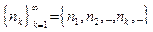 возрастающую последовательность тех натуральных чисел
возрастающую последовательность тех натуральных чисел 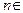 N, для которых
N, для которых 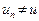 . Теперь уже
. Теперь уже  строго при
строго при 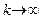 , а для остальных индексов n (то есть при
, а для остальных индексов n (то есть при  ) выполняется равенство
) выполняется равенство 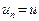 . Рассмотрим такую последовательность
. Рассмотрим такую последовательность  , что
, что 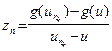 , если существует такое k, что
, если существует такое k, что  , и
, и 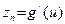 , если
, если 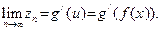 Так как
Так как 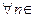 N
N 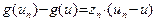 , то
, то
 существует и равен
существует и равен  , что и доказывает формулу
, что и доказывает формулу  .
.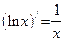 . Имеем:
. Имеем: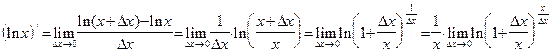 .
. . Применяя 2-й замечательный предел, получаем:
. Применяя 2-й замечательный предел, получаем:  . Используя теперь пункт 2) леммы 1, имеем окончательно:
. Используя теперь пункт 2) леммы 1, имеем окончательно: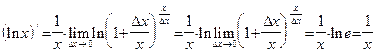 .
. .
.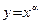 , то
, то  . Дифференцируя обе части полученного равенства и применяя в левой части цепное правило, имеем:
. Дифференцируя обе части полученного равенства и применяя в левой части цепное правило, имеем: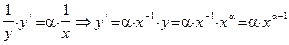 .
. .
. . Имеем:
. Имеем: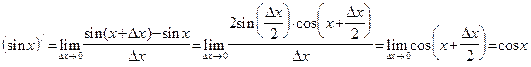 .
. ~
~ 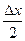 при
при  и непрерывность косинуса, выразившуюся в последнем равенстве.
и непрерывность косинуса, выразившуюся в последнем равенстве. .
.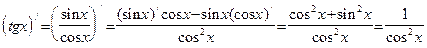 .
. с областью определения D(g) и множеством значений J обратна по отношению к функции
с областью определения D(g) и множеством значений J обратна по отношению к функции 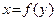 , у которой в точке
, у которой в точке 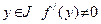 . Тогда в соответствующей точке
. Тогда в соответствующей точке  дифференцируема и справедлива формула:
дифференцируема и справедлива формула: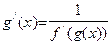 .
.
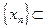 D(g) – произвольная последовательность, строго стремящаяся к x. Из условий леммы следует, что
D(g) – произвольная последовательность, строго стремящаяся к x. Из условий леммы следует, что  , такое, что
, такое, что 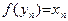 . Отсюда вытекает, что
. Отсюда вытекает, что 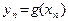 и в силу непрерывности функции g
и в силу непрерывности функции g 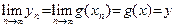 . При этом ясно, что
. При этом ясно, что  строго. Имеем:
строго. Имеем: .
. существует и равен
существует и равен 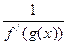 , что и доказывает формулу (17).
, что и доказывает формулу (17). , а
, а  . Известно, что функция
. Известно, что функция 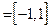 (см. теорему 3), имеет множество значений
(см. теорему 3), имеет множество значений  , на котором определена обратная ей функция
, на котором определена обратная ей функция  . По формуле (17) в соответствующих точках
. По формуле (17) в соответствующих точках  :
: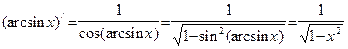 .
.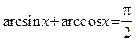 немедленно получаем:
немедленно получаем: .
. , а
, а  . Известно, что функция
. Известно, что функция 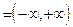 (см. теорему 3), имеет множество значений
(см. теорему 3), имеет множество значений  , на котором определена обратная ей функция
, на котором определена обратная ей функция  . По формуле (17) в соответствующих точках
. По формуле (17) в соответствующих точках 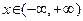 :
: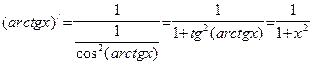 .
. получаем:
получаем: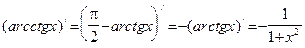 .
.


