Определение предела последовательности
Обозначим через N множество натуральных чисел. Итак, N=  .
.
Определение 2. Последовательностью действительных чисел  называется закон, согласно которому каждому
называется закон, согласно которому каждому 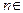 N ставится в соответствие действительное число
N ставится в соответствие действительное число 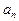 , называемое элементом последовательности. Элемент
, называемое элементом последовательности. Элемент 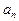 называется общим членом последовательности.
называется общим членом последовательности.
Последовательность чаще всего задается своим общим членом 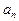 . Более подробно последовательность
. Более подробно последовательность  выписывают так:
выписывают так:  .
.
Пример 2. 1) Расположим элементы последовательности с общим членом  на действительной прямой:
на действительной прямой:

Мы видим, что элементы этой последовательности с ростом n приближаются к точке 0 на сколь угодно малое расстояние. Говорят также, что последовательность  " сгущается" около точки 0, или " стремится" к точке 0. Мы увидим, что в соответствие с точным определением, которое будет дано чуть позже, число 0 является пределом последовательности
" сгущается" около точки 0, или " стремится" к точке 0. Мы увидим, что в соответствие с точным определением, которое будет дано чуть позже, число 0 является пределом последовательности  .
.
2) Рассмотрим теперь следующую последовательность:  . Имеем:
. Имеем: 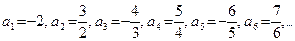 . Нанесем эти элементы на числовую прямую:
. Нанесем эти элементы на числовую прямую:
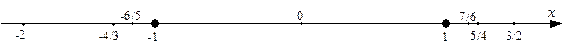
Нечетные элементы этой последовательности сгущаются вокруг точки –1, а четные – вокруг точки 1. То есть не существует одной такой точки, вокруг которой сгущались бы все члены данной последовательности с ростом n. О такого сорта последовательностях говорят, что они не имеют предела (расходятся).
3) Члены последовательности 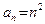 с ростом n уходят все дальше и дальше вправо на числовой прямой:
с ростом n уходят все дальше и дальше вправо на числовой прямой:

О такой последовательности мы будем говорить, что ее предел равен  , или что она расходится к
, или что она расходится к  . Аналогично, о последовательности
. Аналогично, о последовательности  , члены которой с ростом n уходят все дальше и дальше влево на числовой прямой, говорят, что ее предел равен
, члены которой с ростом n уходят все дальше и дальше влево на числовой прямой, говорят, что ее предел равен  , или что она расходится к
, или что она расходится к  .
.
4) Члены последовательности  , перескакивая с одной стороны оси Ox на другую, с ростом n также удаляются на все большее и большее расстояние от начала координат:
, перескакивая с одной стороны оси Ox на другую, с ростом n также удаляются на все большее и большее расстояние от начала координат:
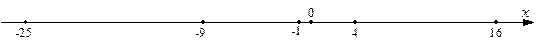
Так как элементы 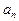 не сохраняют определенный знак, то в этом случае будем говорить, что предел данной последовательности равен
не сохраняют определенный знак, то в этом случае будем говорить, что предел данной последовательности равен 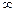 (то есть перед символом
(то есть перед символом 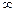 не будем ставить никакой знак).
не будем ставить никакой знак).
Перед тем, как перейти к строгим определениям, напомним обозначения двух логических символов, с помощью которых сокращают некоторые записи. А именно, вместо фраз " для любого", " для всякого", " для каждого" часто записывают символ  ; вместо слов " существует", " существуют" записывают символ
; вместо слов " существует", " существуют" записывают символ  . Кроме того, греческими буквами
. Кроме того, греческими буквами  и
и  мы будем всегда обозначать положительные переменные, могущие принимать сколь угодно малые значения.
мы будем всегда обозначать положительные переменные, могущие принимать сколь угодно малые значения.
Определение 3.  - окрестностью точки
- окрестностью точки  называется множество точек
называется множество точек 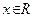 , удовлетворяющих неравенству
, удовлетворяющих неравенству  (которое, как известно, равносильно двойному неравенству
(которое, как известно, равносильно двойному неравенству  ).
).
Геометрически  - окрестность точки
- окрестность точки  представляет собой открытый интервал
представляет собой открытый интервал  числовой прямой:
числовой прямой:
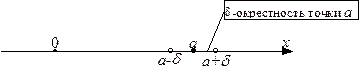
Определение 4. 1) Число  называется пределом последовательности
называется пределом последовательности  , если
, если  (N – натуральное число), такое, что
(N – натуральное число), такое, что  число
число 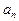 попадает в
попадает в  - окрестность точки a, то есть выполняется неравенство:
- окрестность точки a, то есть выполняется неравенство:
|
|  . .
| (2)
|
Тот факт, что a есть предел  обозначается следующим образом:
обозначается следующим образом: 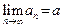 .
.
2) В случае, если не существует числа  , удовлетворяющего пункту 1) данного определения, говорят что последовательность
, удовлетворяющего пункту 1) данного определения, говорят что последовательность  расходится (не имеет конечного предела).
расходится (не имеет конечного предела).
3) Если  (M – сколь угодно большое число)
(M – сколь угодно большое число)  , такое, что
, такое, что 
 (соответственно,
(соответственно,  ), то говорят, что последовательность
), то говорят, что последовательность  расходится к
расходится к  (соответственно, расходится к
(соответственно, расходится к  ), и этот факт обозначают следующим образом:
), и этот факт обозначают следующим образом:  (соответственно,
(соответственно,  ).
).
4) Если  (M – сколь угодно большое число)
(M – сколь угодно большое число)  , такое, что
, такое, что 
 , то говорят, что последовательность
, то говорят, что последовательность  расходится к
расходится к 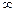 , и этот факт обозначают следующим образом:
, и этот факт обозначают следующим образом:  .
.
Читателю предлагается доказать, что последовательности, взятые из пунктов 1)–4) примера 2, соответственно удовлетворяют пунктам 1)–4) определения 4, то есть, что 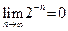 ,
,  не существует,
не существует,  .
.
Свойства предела последовательности
1. Предел константы равен самой этой константе, то есть если 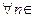 N
N  , то
, то
|
|  . .
|
|
2. Предел суммы двух последовательностей равен сумме пределов этих последовательностей, то есть если  и
и  существуют, то
существуют, то
3. Постоянный множитель можно вынести за знак предела, то есть если 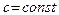 и
и  существует, то
существует, то
|
|   . .
|
|
4. Предел произведения двух последовательностей равен произведению пределов этих последовательностей, то есть если  и
и  существуют, то
существуют, то
|
|   . .
|
|
5. Предел частного двух последовательностей равен частному пределов этих последовательностей, то есть если  и
и  существуют и
существуют и  , то
, то
|
|  . .
|
|
6. Если члены одной последовательности не превышают соответствующих членов другой последовательности, то и предел первой последовательности не превышает предела второй последовательности, то есть если 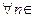 N
N  и пределы
и пределы  и
и  существуют, то
существуют, то
|
|  . .
|
|
Заметим, что если выполняется строгое неравенство  , то после перехода к пределу может получится равенство. Например, если
, то после перехода к пределу может получится равенство. Например, если  , а
, а  , то
, то  , однако
, однако  . Таким образом, в общем случае следствием неравенства
. Таким образом, в общем случае следствием неравенства  является нестрогое неравенство
является нестрогое неравенство  .
.
7. Если  =
=  = a и
= a и 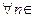 N
N  , то предел последовательности
, то предел последовательности  существует и
существует и
|
|  . .
|
|
8. Если последовательность  ограничена (то есть
ограничена (то есть  , такое, что
, такое, что 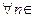 N
N  , а
, а  , то
, то
|
|  . .
|
|
Доказательства свойств 1–6 мы опускаем. Их можно найти в любом учебнике по математическому анализу. Докажем лишь свойства 7 и 8.
Доказательство свойства 7. Пользуясь определением 4, распишем тот факт, что  :
:  . Точно то же сделаем для
. Точно то же сделаем для  :
: 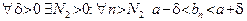 . Положим
. Положим 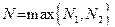 . Тогда при
. Тогда при  два полученные двойные неравенства выполняются одновременно и, следовательно, имеем:
два полученные двойные неравенства выполняются одновременно и, следовательно, имеем:
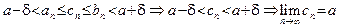 . ˆ
. ˆ
Доказательство свойства 8. Прежде всего отметим, что равенство  равносильно равенству
равносильно равенству  . Имеем:
. Имеем: 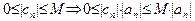 . Так как
. Так как  , то по свойству 7
, то по свойству 7 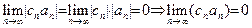 .
.
Монотонные последовательности
Определение 5. Последовательность  называется монотонно возрастающей (соответственно, монотонно убывающей), если
называется монотонно возрастающей (соответственно, монотонно убывающей), если 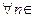 N
N 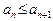 (соответственно,
(соответственно,  ). Если
). Если 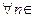 N выполняются соответствующие строгие неравенства, то говорят о строгом возрастании и строгом убывании последовательности.
N выполняются соответствующие строгие неравенства, то говорят о строгом возрастании и строгом убывании последовательности.
Например, в примере 2 последовательность 1) строго монотонно убывает, последовательность 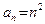 из пункта 3) строго монотонно возрастает, а последовательность 2) не является монотонной. Для монотонных последовательностей справедлива следующая теорема, доказательство которой выходит за рамки нашей программы.
из пункта 3) строго монотонно возрастает, а последовательность 2) не является монотонной. Для монотонных последовательностей справедлива следующая теорема, доказательство которой выходит за рамки нашей программы.
Теорема 1. 1) Если последовательность  монотонно возрастает и ограничена сверху (то есть
монотонно возрастает и ограничена сверху (то есть  , такое, что
, такое, что 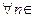 N
N  , то данная последовательность имеет предел, причем
, то данная последовательность имеет предел, причем  .
.
2) Если последовательность  монотонно убывает и ограничена снизу (то есть
монотонно убывает и ограничена снизу (то есть  , такое, что
, такое, что 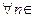 N
N  , то данная последовательность имеет предел, причем
, то данная последовательность имеет предел, причем  . €
. €
Пример 3. Рассмотрим последовательность  . Используя формулу бинома Ньютона и формулу суммы геометрической прогрессии, можно доказать (доказательство не слишком простое), что эта последовательность монотонно возрастает и ограничена сверху числом M =3. По теореме 1 данная последовательность имеет предел, который, следуя Л.Эйлеру, обозначают буквой e. Приближенное значение числа e таково:
. Используя формулу бинома Ньютона и формулу суммы геометрической прогрессии, можно доказать (доказательство не слишком простое), что эта последовательность монотонно возрастает и ограничена сверху числом M =3. По теореме 1 данная последовательность имеет предел, который, следуя Л.Эйлеру, обозначают буквой e. Приближенное значение числа e таково:  .
.
Определение 6. Число
|
|  . .
|
(3)
|
называется числом Эйлера. €
При изучении понятия предела функции нам понадобится следующее
Определение 7. Говорят, что последовательность  строго стремится к числу
строго стремится к числу  , если
, если 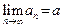 и
и 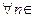 N выполняется неравенство
N выполняется неравенство  . €
. €
Например, последовательность  из пункта 1) примера 2 стремится к нулю строго. Предел же последовательности
из пункта 1) примера 2 стремится к нулю строго. Предел же последовательности 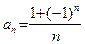 , как это следует из свойства 8 пределов последовательностей, равен нулю. Однако
, как это следует из свойства 8 пределов последовательностей, равен нулю. Однако 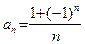 не стремится к нулю строго, так как при нечетных n
не стремится к нулю строго, так как при нечетных n 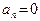 .
.

 .
. называется закон, согласно которому каждому
называется закон, согласно которому каждому 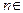 N ставится в соответствие действительное число
N ставится в соответствие действительное число 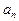 , называемое элементом последовательности. Элемент
, называемое элементом последовательности. Элемент  .
. на действительной прямой:
на действительной прямой:
 . Имеем:
. Имеем: 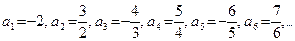 . Нанесем эти элементы на числовую прямую:
. Нанесем эти элементы на числовую прямую: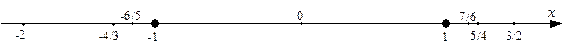
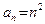 с ростом n уходят все дальше и дальше вправо на числовой прямой:
с ростом n уходят все дальше и дальше вправо на числовой прямой:
 , или что она расходится к
, или что она расходится к  . Аналогично, о последовательности
. Аналогично, о последовательности  , члены которой с ростом n уходят все дальше и дальше влево на числовой прямой, говорят, что ее предел равен
, члены которой с ростом n уходят все дальше и дальше влево на числовой прямой, говорят, что ее предел равен  , или что она расходится к
, или что она расходится к  , перескакивая с одной стороны оси Ox на другую, с ростом n также удаляются на все большее и большее расстояние от начала координат:
, перескакивая с одной стороны оси Ox на другую, с ростом n также удаляются на все большее и большее расстояние от начала координат: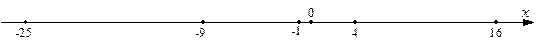
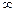 (то есть перед символом
(то есть перед символом  ; вместо слов " существует", " существуют" записывают символ
; вместо слов " существует", " существуют" записывают символ  . Кроме того, греческими буквами
. Кроме того, греческими буквами  и
и  мы будем всегда обозначать положительные переменные, могущие принимать сколь угодно малые значения.
мы будем всегда обозначать положительные переменные, могущие принимать сколь угодно малые значения. называется множество точек
называется множество точек 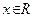 , удовлетворяющих неравенству
, удовлетворяющих неравенству  (которое, как известно, равносильно двойному неравенству
(которое, как известно, равносильно двойному неравенству  ).
). числовой прямой:
числовой прямой: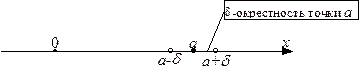
 (N – натуральное число), такое, что
(N – натуральное число), такое, что  число
число  .
.
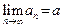 .
. (M – сколь угодно большое число)
(M – сколь угодно большое число)  , такое, что
, такое, что 
 (соответственно,
(соответственно,  ), то говорят, что последовательность
), то говорят, что последовательность  (соответственно,
(соответственно,  ).
). , то говорят, что последовательность
, то говорят, что последовательность  .
.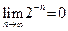 ,
,  не существует,
не существует,  .
.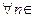 N
N  , то
, то .
.
 и
и  существуют, то
существуют, то
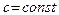 и
и 

 .
.
 , то
, то .
.
 и пределы
и пределы  .
.
 , то после перехода к пределу может получится равенство. Например, если
, то после перехода к пределу может получится равенство. Например, если  , а
, а  , то
, то  . Таким образом, в общем случае следствием неравенства
. Таким образом, в общем случае следствием неравенства  , то предел последовательности
, то предел последовательности  существует и
существует и .
.
 , такое, что
, такое, что  , а
, а  , то
, то .
.
 :
:  . Точно то же сделаем для
. Точно то же сделаем для  :
: 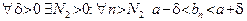 . Положим
. Положим 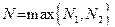 . Тогда при
. Тогда при  два полученные двойные неравенства выполняются одновременно и, следовательно, имеем:
два полученные двойные неравенства выполняются одновременно и, следовательно, имеем: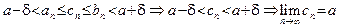 . ˆ
. ˆ . Имеем:
. Имеем: 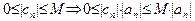 . Так как
. Так как  , то по свойству 7
, то по свойству 7 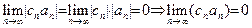 .
.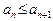 (соответственно,
(соответственно,  ). Если
). Если  , такое, что
, такое, что  , то данная последовательность имеет предел, причем
, то данная последовательность имеет предел, причем  .
. , такое, что
, такое, что  , то данная последовательность имеет предел, причем
, то данная последовательность имеет предел, причем  . €
. € . Используя формулу бинома Ньютона и формулу суммы геометрической прогрессии, можно доказать (доказательство не слишком простое), что эта последовательность монотонно возрастает и ограничена сверху числом M =3. По теореме 1 данная последовательность имеет предел, который, следуя Л.Эйлеру, обозначают буквой e. Приближенное значение числа e таково:
. Используя формулу бинома Ньютона и формулу суммы геометрической прогрессии, можно доказать (доказательство не слишком простое), что эта последовательность монотонно возрастает и ограничена сверху числом M =3. По теореме 1 данная последовательность имеет предел, который, следуя Л.Эйлеру, обозначают буквой e. Приближенное значение числа e таково:  .
. .
.
 . €
. €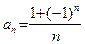 , как это следует из свойства 8 пределов последовательностей, равен нулю. Однако
, как это следует из свойства 8 пределов последовательностей, равен нулю. Однако 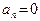 .
.


