Ошибки, вызванные помехой f(t)
В рассматриваемой работе предполагается: · задающее воздействие x (t) является регулярным, · помеха f (t) – случайный процесс с нулевым математическим ожиданием. Учитывая принцип суперпозиции, результирующая ошибка ε уст (t) складывается из рассчитанной ранее регулярной ε рег(t) и случайной ε сл (t) составляющих. Изображение случайной составляющей для системы, представленной структурной схемой, изображенной на рис. 1.1, определяется выражением [3, стр. 321-322].
Рассматриваемые системы являются линейными и стационарными. Помеха f (t) – достаточно широкополосный случайный процесс, чтобы её можно было описывать как белый шум. Математической моделью белого шума является случайный стационарный процесс с нулевым математическим ожиданием и спектральной плотностью мощности В этих условиях ошибка eсл(t) в установившемся режиме также представляет собой стационарный случайный процесс с нулевым математическим ожиданием и спектральной плотностью:
Дисперсия случайной ошибки eсл(t) определяется выражением
Формулы для вычисления интегралов вида:
приведены в [3, стр. 321-322]. При n = 3 полиномы в выражении (2.15) имеют вид С (j w) = с 0 + с 1 j w + с 2(j w)2, D (j w) = d 0 + d 1 j w + d 2(j w)2 + d 3(j w)3. Следует обратить внимание на совмещение обозначений: C (s) - знаменатель передаточной функции системы W (s) в разомкнутом состоянии, С (j w) - числитель комплексного коэффициента передачи K ε f (j w) в формуле (2/13). Кроме этого, при записи полиномов С (j w) и D (j w) изменен порядок индексации коэффициентов ci: i = 0, 1, 2 и dj: j = 0, 1, 2, 3. Таким образом, для систем третьего порядка (n = 3):
Удобно дисперсию ошибки представлять в виде
где D F э - эквивалентная шумовая полоса рассматриваемой системы, равная полосе пропускания некоторой эквивалентной системы, имеющей прямоугольную амплитудно-частотную характеристику (АЧХ) системы в замкнутом состоянии А з = А з (ω) (см. рис.2.1) с тем же коэффициентом передачи на нулевой частоте, что и в рассматриваемой системе. Для статических систем значение А з (0) = К ε f (0) =
 . (2.18) . (2.18)
Именно значение D F э характеризует помехоустойчивость системы. Чем шире полоса D F э, тем меньше помехоустойчивость системы. 1. Статическая система:
Следовательно,
и, выделив сомножители, содержащие коэффициент k,
|

 ,
, (2.12)
(2.12)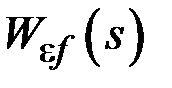 – передаточная функция ошибки системы по помехе f (t).
– передаточная функция ошибки системы по помехе f (t). . В рассматриваемом случае
. В рассматриваемом случае 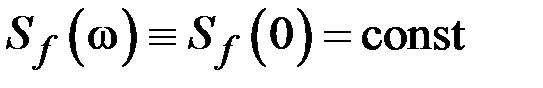 , где
, где  – значение спектральной плотности помехи на нулевой частоте.
– значение спектральной плотности помехи на нулевой частоте. ,
,  (2.13)
(2.13) . (2.14)
. (2.14) , (2.15)
, (2.15) . (2.16)
. (2.16) , (2.17)
, (2.17) и, следовательно, при k > > 1 близко к единице, для астатических систем А з (0) = К ε f (0) = 1.
и, следовательно, при k > > 1 близко к единице, для астатических систем А з (0) = К ε f (0) = 1.
 ,
, .
. ,
,  ,
, ,
,  ,
, 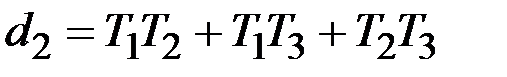 ,
, 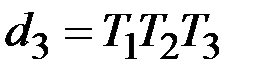 ,
,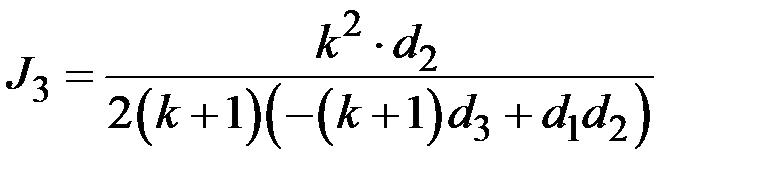 . (2.19)
. (2.19)


