Ошибки по регулярному задающему воздействию
Точность системы определяется величиной ошибки e(t). Определить закон изменения функции e = e(t) в течение времени переходного процесса (динамическую ошибку) так же сложно, как и временные характеристики. Гораздо проще найти ошибку в установившемся режиме работы системы (для моментов времени много больших времени переходного процесса, т.е. t > > tn) В дальнейшем будут рассмотрены только ошибки в установившемся режиме работы системы. Регулярное задающее воздействие удобно представить в виде его разложения по степеням времени t
a – постоянная составляющая входного воздействия, v – его скорость, w – ускорение. Точность системы характеризуется значениями ошибок, вычисляемых для трех пробных регулярных входных воздействий: · · · Передаточная функция W (s) системы третьего порядка (n = 3) в разомкнутом состоянии представляется как отношение полиномов (здесь m = 1) W (s) = Тогда в соответствии со структурной схемой рис.1.1 передаточная функция ошибки системы по регулярному задающему воздействию представляется в виде:
Передаточная функция ошибки системы позволяет определить изображение ошибки
Для расчета характеристик точности системы используется достаточно простой, приближенный метод – метод коэффициентов ошибок. Преобразование (2.3) значительно упрощается, если передаточную функцию ошибки W e x (s) представить в виде разложения по степеням s относительно точки s = 0 (в установившемся режиме работы системы при
где g0, g1, g2 – коэффициенты ошибок по постоянной составляющей задающего воздействия x (t), по его скорости и ускорению, соответственно. С учетом разложения (2.4) выражение для изображения ошибки приобретает вид
что позволяет, применяя обратное преобразование Лапласа к обеим частям полученного уравнения, получить формулу для вычисления регулярных ошибок системы
Следовательно, для трех введенных ранее пробных входных воздействий имеем
Для нахождения коэффициентов ошибок g0, g1, g2 составляются уравнения, получаемые приравниванием коэффициентов при одинаковых степенях s левой и правой частей соотношения, получаемого из выражений (2.2) и (2.4).
Итак, формируются три уравнения для определения коэффициентов ошибок g0, g1, g2. 1. 2. 3.
1. Для статической системы соотношение (2.7) представляется в виде:
Таким образом:
и, после некоторых преобразований имеем:
2. Для астатической системы первого порядка астатизма соотношение (2.7) имеет вид
и, следовательно:
1. Для астатической системы второго порядка астатизма для выражения (2.7) получим
следовательно,
Анализ полученных результатов позволяет сделать следующие выводы: 1. Для повышения точности системы следует повышать ее порядок астатизма. В соответствии с формулами (2.10) и (2.11) статические ошибки астатических систем всегда равны нулю, так как g0 = 0 (статической называется ошибка по постоянной составляющей входного воздействия, то есть при х (t) º a). Для астатической системы второго порядка ошибка и по скорости входного воздействия равна нулю, так как и g1 = 0. 2. Для системы любой структуры для повышения точности следует повышать коэффициент усиления k системы в разомкнутом состоянии.
|

 ,
,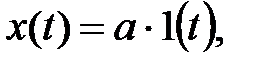 a = const – постоянная составляющая,
a = const – постоянная составляющая, v = const – скорость входного воздействия,
v = const – скорость входного воздействия,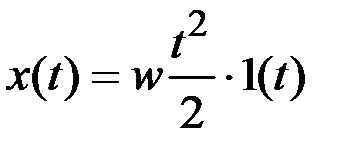 , w = const – ускорение входного воздействия.
, w = const – ускорение входного воздействия. (2.1)
(2.1)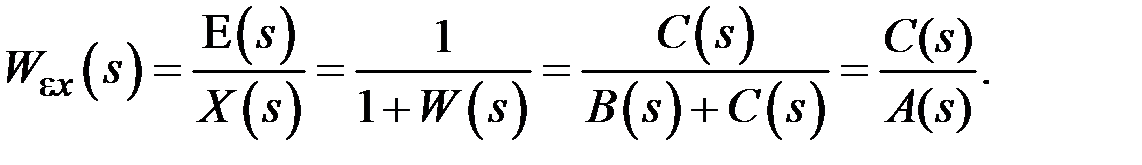 (2.2)
(2.2) и после применения обратного преобразования Лапласа – ошибку в установившемся режиме
и после применения обратного преобразования Лапласа – ошибку в установившемся режиме 
 (2.3)
(2.3) ).
). , (2.4)
, (2.4) ,
, ,
,  . (2.5)
. (2.5) ,
, ,
,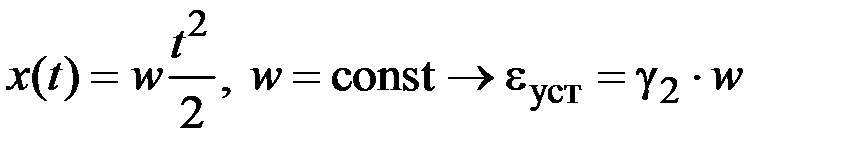 . (2.6)
. (2.6)

 . (2.7)
. (2.7) ,
, ,
,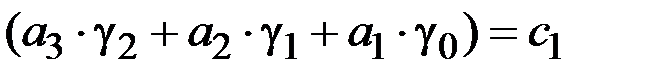 . (2.8)
. (2.8) .
. ,
,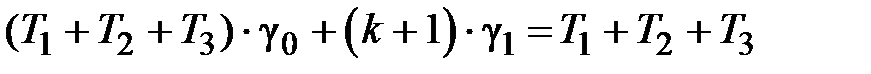 ,
,
 ,
,  ,
, . (2.9)
. (2.9)
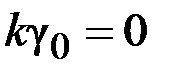 ,
,  ,
,  ,
,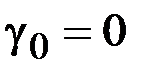 ,
, 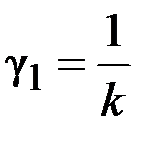 ,
,  . (2.10)
. (2.10)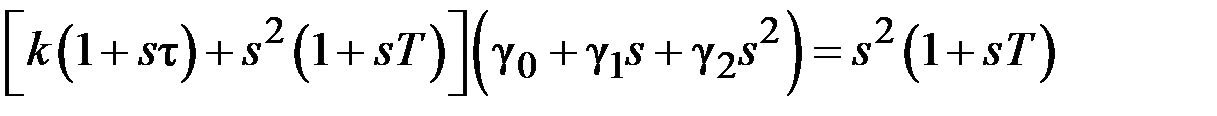 ,
,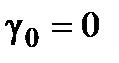 ,
,  ,
,  . (2.11)
. (2.11)


