Идеальное интегрирующее звено. J(w) = – arctg wT. Таблица 1.2 w ¥ ϕ(w) –6° –11°. J(w) = – arctg wT. Таблица 1.2 w ¥ ϕ(w) –6° –11°
где k – коэффициент усиления; T – постоянная времени звена.
График L = L (w) логарифмической амплитудно-частотной характеристики интегрирующего звена (учитывая логарифмический масштаб по оси w) представляет собой прямую с наклоном - 20 дБ/дек во всей области частот (0£ w < ¥), пересекающую ось w на частоте w = k.
Рис.1.6. ЛАХ интегрирующего звена (Наклон - 20 дБ/дек означает, что при увеличении частоты в 10 раз (на декаду) величина L (w) уменьшится на 20 дБ). Логарифмическая фазочастотная характеристика во всей области частот равна - 90° (j(w) = - 90°).На рис. 1.6 точно один под другим изображены графики ЛАХ интегрирующего звена.
3. Инерционное звено имеет передаточную функцию
где k – коэффициент усиления; T – постоянная времени звена. Значения этих параметров для инерционного звенане зависят друг от друга. Для идеального инерционного звена коэффициент усиления k = 1. Комплексный коэффициент передачи звена и его характеристики:
Второе слагаемое в выражении (1.15) (т.е. Таким образом, асимптотические логарифмические характеристики идеального инерционного звена имеют вид (учитывая единичный коэффициент усиления L (w) = 20lg(A (w)) = j(w) = – arctg w T.
График асимптотической амплитудно-частотной характеристики L (w) идеального инерционного звена представляет собой ломаную линию, совпадающую с осью w в диапазоне изменения частот от нуля до частоты сопряжения wcon =
Рис. 1.7. ЛАХ идеального инерционного звена График фазочастотной характеристики инерционного звена строится в соответствии с табл. 1.2. j(w) = – arctg w T. Таблица 1.2
|

 , (1.11)
, (1.11) ,
,  ,
,  . (1.12)
. (1.12)
 , (1.13)
, (1.13) ,
,  ,
,  , (1.14)
, (1.14) . (1.15)
. (1.15) при k = 1) имеет хорошее приближение в виде линейно-ломанной кривой, асимптотически приближающейся к истинной кривой на малых и больших частотах.
при k = 1) имеет хорошее приближение в виде линейно-ломанной кривой, асимптотически приближающейся к истинной кривой на малых и больших частотах. и постоянную времени T)
и постоянную времени T) , (1.16)
, (1.16)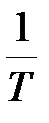 , и наклонную прямую с наклоном - 20 дБ/дек, длячастот, больших частоты сопряжения(рис.1.7).
, и наклонную прямую с наклоном - 20 дБ/дек, длячастот, больших частоты сопряжения(рис.1.7).










