Расположению корней на комплексной плоскости
Системы первого порядка (n = 1) Если единичной обратной связью охватить идеальное интегрирующее звено, то передаточная функция системы в замкнутом состоянии описывается как инерционное звено и может рассматриваться в качестве модели системы первого порядка. Такая система называется астатической системой первого порядка астатизма, поскольку её передаточная функция в разомкнутом состоянии W (s) содержит одно интегрирующее звено.
Передаточная функция системы первого порядка формируется и в том случае, когда единичной обратной связью охватывается идеальное инерционное звено. В этом случае система называется статической (передаточная функция в разомкнутом состоянии W (s) не содержит интегрирующих звеньев).
В обоих случаях характеристическое уравнение системы
Системы второго порядка (n = 2) Если обратной связью охватить реальное интегрирующее звено с передаточной функцией
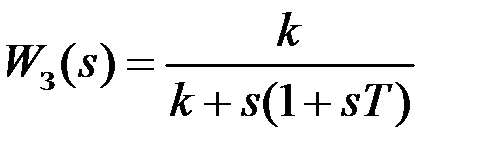 (1.5) (1.5)
Приравнивая нулю знаменатель передаточной функции (1.5), получаем характеристическое уравнение
В случае, когда выполняется неравенство 4kТ < 1, корни характеристического уравнения s1, s2 – вещественные и отрицательные (см. рис 1.2),
и система представляется как апериодическое звено второго порядка
Если 4 kТ > 1, то корни уравнения (1.6) – комплексно-сопряженные
На рис. 1.3 представлено расположение корней характеристического уравнения на комплексной плоскости для колебательного звена.
Заключение 1. Характер и показатели качества переходного процесса исключительно зависят от типа корней характеристического уравнения системы. 2. Система устойчива, если все ее вещественные корни отрицательны, а все комплексно-сопряженные корни имеют отрицательные вещественные части. Таким образом, устойчивые корни находятся в левой полуплоскости комплексной плоскости. Мнимая ось является границей устойчивости. 3. Быстродействие системы оценивается по времени переходного процесса tп точно или приближенно равным tп = 4. Колебательный характер переходного процесса вызывается наличием комплексно-сопряженных корней. Колебательностьтем выше, чем больше мнимая часть комплексных корней по отношению к их вещественной части. 5. Колебательность рассматривается как мера запаса устойчивости системы (чем выше колебательность, тем меньше запас устойчивости).
|

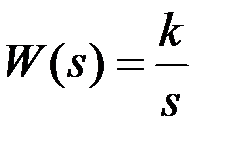 ,
, 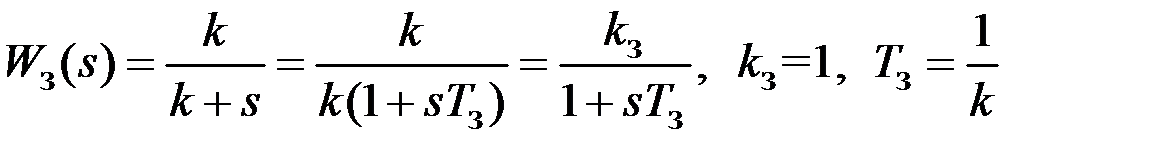 . (1.3)
. (1.3) . (1.4)
. (1.4)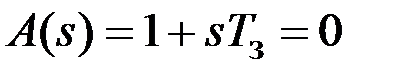 имеет один отрицательный (и поэтому устойчивый) вещественный корень
имеет один отрицательный (и поэтому устойчивый) вещественный корень  .
. , то в зависимости от соотношения значений параметров k и T, передаточная функция системы в замкнутом состоянии представляется колебательным или апериодическим звеном второго порядка. Действительно, в соответствии с выражением (1.2) имеем
, то в зависимости от соотношения значений параметров k и T, передаточная функция системы в замкнутом состоянии представляется колебательным или апериодическим звеном второго порядка. Действительно, в соответствии с выражением (1.2) имеем
 , решением которого являются два корня
, решением которого являются два корня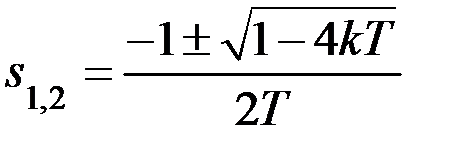 . (1.6)
. (1.6) ,
,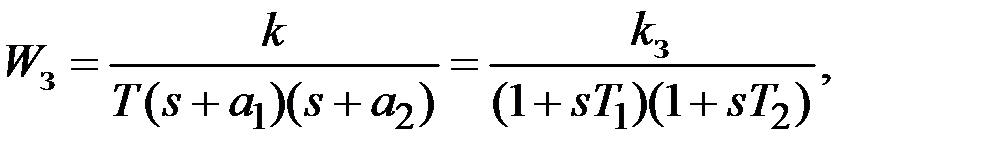
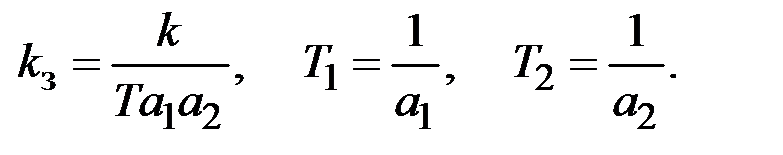
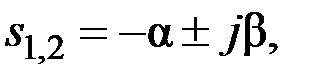
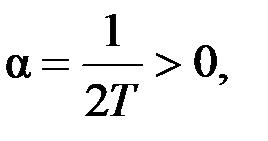
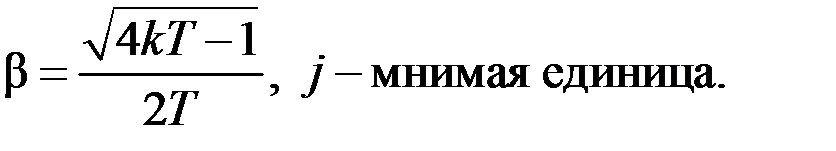
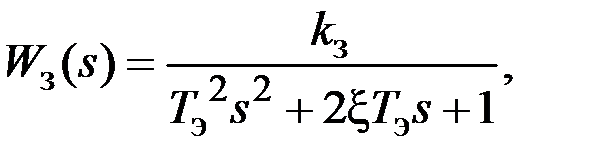
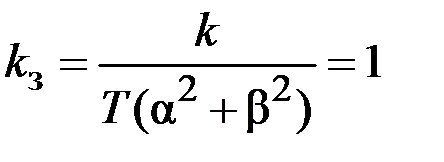 ,
,
 .
.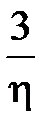 , где h – расстояние до мнимой оси ближайшего к ней корня характеристического уравнения.
, где h – расстояние до мнимой оси ближайшего к ней корня характеристического уравнения.


