Модели линейных непрерывных систем
Уральский технический институт связи и информатики (филиал)
Структурная схема изучаемых следящих систем представлена на рис. 1.1. Здесь х(t) – регулярное задающее воздействие; y(t) – выходная (регулируемая) величина; ε (t) = x(t) - y(t) – ошибка системы; f (t) – случайная помеха;
Математические модели отдельных элементов систем или всей системы представляются в виде определенного набора динамических звеньев. Динамическими называются непрерывные системы или элементы систем, которые могут быть описаны с помощью обыкновенных дифференциальных уравнений. В предлагаемой работе изучается следующий набор звеньев, заданных передаточными функциями:
k – коэффициенты усиления звеньев, Т, Т1, T2 – постоянные времени звеньев, ξ – коэффициент демпфирования колебательного звена. Параметры k, Т, Т1, T2, ξ – заданные постоянные величины. Все приведенные звенья либо определяют передаточную функцию W(s), либо являются частью ее. Инерционное, колебательное и апериодическое звено второго порядка могут описывать и систему в замкнутом состоянии (это отражено в обозначении передаточных функций последних двух звеньев) Передаточная функция W(s) представляется в виде отношения двух полиномов В(s) и C(s) комплексной переменной s с постоянными коэффициентами порядка m и n, соответственно, т. е.
|

 – передаточная функция системы в разомкнутом состоянии.
– передаточная функция системы в разомкнутом состоянии. – передаточная функция системы в замкнутом состоянии;
– передаточная функция системы в замкнутом состоянии;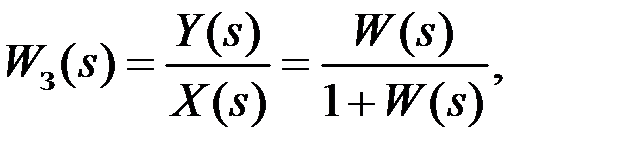 (1.1)
(1.1) ,
,  – идеальное интегрирующее звено;
– идеальное интегрирующее звено;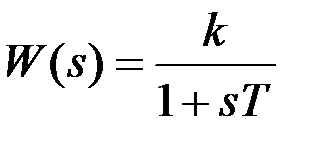 – инерционное звено или апериодическое звено первого порядка. В частном случае, когда коэффициент k равен единице (k = 1), такое звено называется идеальным;
– инерционное звено или апериодическое звено первого порядка. В частном случае, когда коэффициент k равен единице (k = 1), такое звено называется идеальным; – реальное интегрирующее звено;
– реальное интегрирующее звено; 0 < ξ < 1 – колебательное звено;
0 < ξ < 1 – колебательное звено;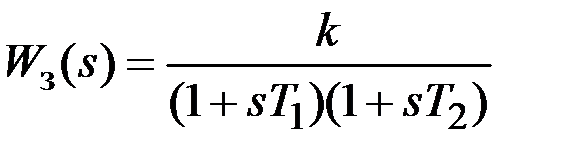 – апериодическое звено второго порядка,
– апериодическое звено второго порядка, . Тогда передаточная функция системы в замкнутом состоянии в соответствии с формулой (1.1) будет иметь вид
. Тогда передаточная функция системы в замкнутом состоянии в соответствии с формулой (1.1) будет иметь вид A(s) = B(s) + C(s), (1.2)
A(s) = B(s) + C(s), (1.2)
 ,
, .
.


