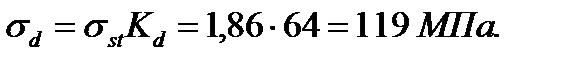Частные случаи
1. Если h = 0, т. е. имеет место внезапное приложение нагрузки, то из формул (10.12) и (10.13) получим 2. Если высота падения h значительно больше статической деформации
Пример. На стальную двутавровую балку № 27а пролетом 3 м падает посередине пролета груз G = 1 кН с высотой h = 10 cм = 0, 1 м. Момент инерции сечения Определить наибольший прогиб балки и максимальные напряжения в ее поперечном сечении. Решение. Вычисляем статический прогиб балки под грузом
Динамический коэффициент
В данном случае динамический эффект падающего груза в 64 раза превосходит его статический эффект. Вычисляем статическое напряжение от груза G. Наибольший изгибающий момент будет в среднем сечении балки:
Наибольшее статическое напряжение
Наибольшее динамическое напряжение
Из этого примера видно, насколько опасными по своему действию являются динамические нагрузки. К этому добавляется еще и то обстоятельство, что допускаемые напряжения при ударе принимают более низкими, чем при действии статических нагрузок.
|
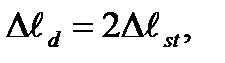
. При внезапном приложении нагрузки деформации и напряжения вдвое больше, чем при статическом действии той же нагрузки.
то для определения динамического коэффициента получим следующую приближенную формулу: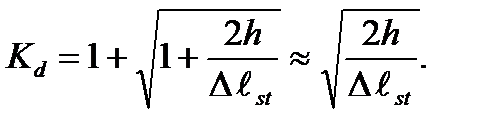
(10.15)
= 5500× 10-8 м4, момент сопротивления Wх =407× 10-6 м3 (из таблиц сортамента); Е =2× 105 MПa.
. (10.16)
(10.17)
.
