Определение перемещений и напряжений при ударе
Рассмотрим случай продольного удара груза по неподвижному телу. Пусть груз весом G падает с высоты h на неподвижный стержень (рис. 10.3 а). Скорость тела в момент удара определяется по известной формуле свободного падения V =(2gh)0, 5. Эта скорость за очень короткий промежуток времени удара, исчисляемый тысячными или сотыми долями секунды, упадет до нуля. Благодаря большому ускорению (замедлению) возникает значительная сила инерции, которая определяет действие удара. Однако теоретически трудно установить закон изменения скорости, а следовательно, и силу инерции. Здесь применяется другой путь, основанный на приближенном использовании закона сохранения энергии и на следующих допущениях: 1) Напряжения при ударе не превосходят предела пропорциональности, так что закон Гука при ударе сохраняет свою силу; 2) Тела после удара не отделяются друг от друга; 3) Масса ударяемого стержня считается малой по сравнению с массой ударяющего тела, поэтому в расчет не принимается;
Рис. 10.3.
4) Потерей части энергии, перешедшей в теплоту и в энергию колебательного движения соударяющихся тел, пренебрегаем. Приравняем работу падающего груза потенциальной энергии деформации стержня. Работа, совершаемая весом падающего груза,
где
Из этих двух уравнений получаем
или
Разделив все члены этого уравнения на ЕА, получим
Но Тогда
Решив это квадратное уравнение относительно
Оставляя знак плюс (так как
где Kd - динамический коэффициент. Разделив обе части последнего уравнения на длину стержня и умножив на модуль упругости Е, перейдем на основании закона Гука от деформаций к напряжениям:
Из этих формул видно, что динамические напряжения и перемещения зависят от статической деформации ударяемого тела. Чем больше статическая деформация (при прочих равных условиях), тем меньше динамические напряжения. Вот почему для смягчения удара применяют прокладки (резиновые, пружинные), дающие большие деформации. При сжимающем ударе во избежание продольного изгиба динамические напряжения не должны превосходить критических напряжений Аналогичный вид имеют формулы и для случая поперечного (изгибающего) удара, только в этом случае вместо
|


 (10.5)
(10.5) - перемещение в точке удара, равное укорочению стержня. Потенциальная энергия деформации при сжатии
- перемещение в точке удара, равное укорочению стержня. Потенциальная энергия деформации при сжатии (10.6)
(10.6) (10.7)
(10.7) (10.8)
(10.8) (10.9)
(10.9) -укорочение стержня от статически приложенной нагрузки G.
-укорочение стержня от статически приложенной нагрузки G. (10.10)
(10.10) , получим
, получим (10.11)
(10.11)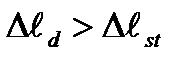 ), получаем окончательно
), получаем окончательно (10.13)
(10.13) (10.14)
(10.14) следует принимать статический прогиб, балки в месте удара -
следует принимать статический прогиб, балки в месте удара -  , а вместо
, а вместо  - динамический прогиб -
- динамический прогиб - 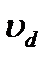 (рис. 10.3 б).
(рис. 10.3 б).


