Практическая формула для расчета на устойчивость
Вместо двух формул (Эйлера и Ясинского), каждая из которых пригодна для определенного диапазона гибкостей, удобнее иметь одну формулу, которой можно было бы пользоваться при любой гибкости стержня.
Эта практическая формула, широко применяющаяся при расчете строительных конструкций, имеет вид
 (9.12) (9.12)
где  - основное допускаемое напряжение на сжатие; - основное допускаемое напряжение на сжатие;  - коэффициент уменьшения основного допускаемого напряжения (или коэффициент продольного изгиба). Величина - коэффициент уменьшения основного допускаемого напряжения (или коэффициент продольного изгиба). Величина  зависит от материала и гибкости стержня. Его значения приведены в табл. 9.1; А - площадь поперечного сечения стержня. зависит от материала и гибкости стержня. Его значения приведены в табл. 9.1; А - площадь поперечного сечения стержня.
Величина  может рассматриваться как допускаемое напряжение при расчете на устойчивость, т.е. может рассматриваться как допускаемое напряжение при расчете на устойчивость, т.е.
 (9.13) (9.13)
Основное допускаемое напряжение на сжатие имеет вид:
 (9.14) (9.14)
где  - предельное напряжение, принимаемое равным пределу текучести для пластичных материалов или пределу прочности для хрупких материалов. - предельное напряжение, принимаемое равным пределу текучести для пластичных материалов или пределу прочности для хрупких материалов.
Связь между коэффициентом  , критическим напряжением , критическим напряжением 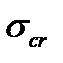 предельным напряжением предельным напряжением  и коэффициентами запаса прочности n и устойчивости и коэффициентами запаса прочности n и устойчивости  , можно установить следующим образом: , можно установить следующим образом:
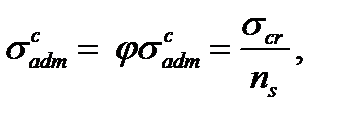
откуда
 (9.15) (9.15)
Используя формулу (9.14), получим
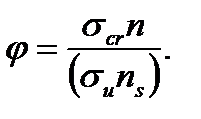 (9.16) (9.16)
Для подбора сечения формулу приводят к следующему виду:
 (9.17) (9.17)
При этом значением ( приходится задаваться, так как гибкость λ неизвестна, ибо неизвестна площадь, сечения A, а гибкость зависит от нее. В качестве, imin, λ по табл. 9.1 находят соответствующее значение ( приходится задаваться, так как гибкость λ неизвестна, ибо неизвестна площадь, сечения A, а гибкость зависит от нее. В качестве, imin, λ по табл. 9.1 находят соответствующее значение ( ) первого приближения рекомендуется принимать ) первого приближения рекомендуется принимать  =0, 5. =0, 5.
Затем определяют величины А,  min. min.
Если получается большая разница между значениями  и и  то следует повторить расчет, задавшись новым значением ( то следует повторить расчет, задавшись новым значением ( ): ):
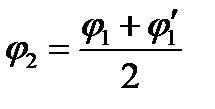
и т.д., пока разница между последовательными значениями не будет превышать 4-6 %.
Для стержней, сечения которых имеют значительные ослабления (например, от отверстий), кроме расчета на устойчивость должен производиться и обычный расчет на прочность по формуле
 (9.18) (9.18)
где Аnt - рабочая (нетто) площадь сечения стержня.
При расчете же на устойчивость берется полная площадь сечения Аbr.
В некоторых случаях (например, при расчете элементов машиностроительных конструкций) значения коэффициентов запаса устойчивости ns, предусмотренные при составлении таблиц коэффициентов  (ns=1, 8), недостаточны. (ns=1, 8), недостаточны.
В этих случаях расчет следует вести, исходя непосредственно из требуемого коэффициента ns и пользуясь формулой Эйлера или Ясинского. Так же следует поступать при расчете на устойчивость стержней из материалов, которые не отражены в таблице коэффициентов  . .
Таблица 9.1.
Гибкость 
|  для для
| | сталей Ст.1, Ст.2, Ст.3, Ст.4
| стали Ст.5
| Стали повышенного качества 
| чугуна
| дерева
| |
| 1, 00
0, 99
0, 96
0, 94
0, 92
0, 89
0, 86
0, 81
0, 75
0, 69
0, 60
0, 52
0, 45
0, 40
0, 36
0, 32
0, 29
0, 26
0, 23
0, 21
0, 19
| 1, 00
0, 98
0, 95
0, 92
0, 89
0, 86
0, 82
0, 76
0, 70
0, 62
0, 51
0, 43
0, 37
0, 33
0, 29
0, 26
0, 24
0, 21
0, 19
0, 17
0, 16
| 1, 00
0, 97
0, 95
0, 91
0, 87
0, 83
0, 79
0, 72
0, 65
0, 55
0, 43
0, 35
0, 30
0, 26
0, 23
0, 21
0, 19
0, 17
0, 15
0, 14
0, 13
| 1, 00
0, 97
0, 91
0, 81
0, 69
0, 57
0, 44
0, 34
0, 26
0, 20
0, 16
-
-
-
-
-
-
-
-
-
-
| 1, 00
0, 99
0, 97
0, 93
0, 87
0, 80
0, 71
0, 60
0, 48
0, 38
0, 31
0, 25
0, 22
0, 18
0, 16
0, 14
0, 12
0, 11
0, 10
0, 09
0, 08
|

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|

Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|
Определение трудоемкости работ и затрат машинного времени На основании ведомости объемов работ по объекту и норм времени ГЭСН составляется ведомость подсчёта трудоёмкости, затрат машинного времени, потребности в конструкциях, изделиях и материалах (табл...
Гидравлический расчёт трубопроводов Пример 3.4. Вентиляционная труба d=0,1м (100 мм) имеет длину l=100 м. Определить давление, которое должен развивать вентилятор,
если расход воздуха, подаваемый по трубе, . Давление на выходе . Местных сопротивлений по пути не имеется. Температура...
Огоньки» в основной период В основной период смены могут проводиться три вида «огоньков»: «огонек-анализ», тематический «огонек» и «конфликтный» огонек...
|
Факторы, влияющие на степень электролитической диссоциации Степень диссоциации зависит от природы электролита и растворителя, концентрации раствора, температуры, присутствия одноименного иона и других факторов...
Йодометрия. Характеристика метода Метод йодометрии основан на ОВ-реакциях, связанных с превращением I2 в ионы I- и обратно...
Броматометрия и бромометрия Броматометрический метод основан на окислении восстановителей броматом калия в кислой среде...
|
|

 (9.12)
(9.12) - основное допускаемое напряжение на сжатие;
- основное допускаемое напряжение на сжатие;  - коэффициент уменьшения основного допускаемого напряжения (или коэффициент продольного изгиба). Величина
- коэффициент уменьшения основного допускаемого напряжения (или коэффициент продольного изгиба). Величина  зависит от материала и гибкости стержня. Его значения приведены в табл. 9.1; А - площадь поперечного сечения стержня.
зависит от материала и гибкости стержня. Его значения приведены в табл. 9.1; А - площадь поперечного сечения стержня. может рассматриваться как допускаемое напряжение при расчете на устойчивость, т.е.
может рассматриваться как допускаемое напряжение при расчете на устойчивость, т.е. (9.13)
(9.13) (9.14)
(9.14) - предельное напряжение, принимаемое равным пределу текучести для пластичных материалов или пределу прочности для хрупких материалов.
- предельное напряжение, принимаемое равным пределу текучести для пластичных материалов или пределу прочности для хрупких материалов. , критическим напряжением
, критическим напряжением 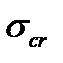 предельным напряжением
предельным напряжением  и коэффициентами запаса прочности n и устойчивости
и коэффициентами запаса прочности n и устойчивости  , можно установить следующим образом:
, можно установить следующим образом: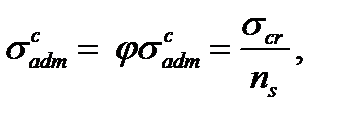
 (9.15)
(9.15)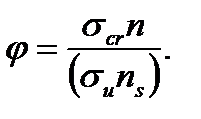 (9.16)
(9.16) (9.17)
(9.17) приходится задаваться, так как гибкость λ неизвестна, ибо неизвестна площадь, сечения A, а гибкость зависит от нее. В качестве, imin, λ по табл. 9.1 находят соответствующее значение (
приходится задаваться, так как гибкость λ неизвестна, ибо неизвестна площадь, сечения A, а гибкость зависит от нее. В качестве, imin, λ по табл. 9.1 находят соответствующее значение ( ) первого приближения рекомендуется принимать
) первого приближения рекомендуется принимать  =0, 5.
=0, 5. min.
min. и
и  то следует повторить расчет, задавшись новым значением (
то следует повторить расчет, задавшись новым значением ( ):
):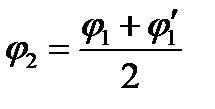
 (9.18)
(9.18) (ns=1, 8), недостаточны.
(ns=1, 8), недостаточны. .
.
 для
для




