Пределы применимости формулы Эйлера
Формулой Эйлера не всегда можно пользоваться. При ее выводе мы пользовались дифференциальным уравнением упругой линии, вывод которого основан на законе Гука. Закон же Гука, как известно, справедлив до тех пор, пока напряжения не превосходят предела пропорциональности. Чтобы установить пределы применимости формулы Эйлера, определим критическое напряжение
где А - площадь поперечного сечения стержня. Но
Величина Таким образом, обозначая
Чтобы можно было пользоваться формулой Эйлера, необходимо удовлетворить следующему условию:
где Записывая формулу (9.9) относительно гибкости, получаем условие применимости формулы Эйлера в виде
Например, для стали Ст.З
Таким образом, для стержней из малоуглеродистой стали формула Эйлера применима, если их гибкость больше 100. Аналогичным образом получим условия применимости формулы Эйлера для чугуна λ ³ 80. Для средне и высокоуглеродистых, а также для легированных сталей формула Эйлера применима и при гибкости, меньшей указанной. Так для стержней из хромомолибденовой стали формула Эйлера применима при λ ³ 70.
|
, т. е. напряжение, возникающее в поперечном сечении стержня при действии критической нагрузки:
(9.8)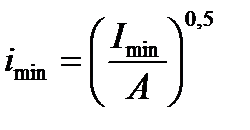
- наименьший радиус инерции поперечного сечения стержня. Поэтому формулу (9.8) можно записать в виде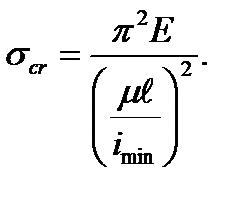
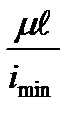характеризует влияние размеров стержня и способа закрепления концов; она называется гибкостью стержня и обозначается λ. Гибкость - величина безразмерная.
получаем
(9.9)
- предел пропорциональности материала стержня.
(9.10)
=200 МПа и
