РАСЧЕТ ТОНКОСТЕННЫХ СОСУДОВ
В технике часто встречаются сосуды, стенки которых воспринимают давление жидкостей, газов и сыпучих тел (паровые котлы, резервуары, рабочие камеры двигателей, цистерны и т. п.). Если сосуды имеют форму тел вращения и толщина стенок их незначительна, а нагрузка осесимметрична, то определение напряжений, возникающих в их стенках под нагрузкой, производится весьма просто. В таких случаях без большой погрешности можно принять, что в стенках возникают только нормальные напряжения (растягивающие или сжимающие) и что эти напряжения распределяются равномерно по толщине стенки. Расчеты, основанные на таких допущениях, хорошо подтверждаются опытами, если толщина стенки не превосходит примерно Вырежем из стенки сосуда элемент с размерами Толщину стенки обозначим t (рис. 8.1). Радиусы кривизны поверхности сосуда в данном месте
Рис. 8.1.
Заменим взаимодействие элемента с оставшейся частью сосуда внутренними силами, интенсивность которых равна Составим условие равновесия элемента, для чего спроецируем силы, действующие на элемент, на направление нормали пп к поверхности элемента. Проекция нагрузки равна Спроецировав все силы, приложенные к выделенному элементу, на направление нормали пп, получим
Ввиду малости размеров элемента можно принять
С учетом этого из уравнения равновесия получим
Учитывая, что d
Сократив на
Эта формула называется формулой Лапласа. Рассмотрим расчет двух видов сосудов, часто встречающихся на практике: сферического и цилиндрического. При этом ограничимся случаями действия внутреннего газового давления.
Рис. 8.2. 1. Сферический сосуд. В этом случае
Так как в данном случае имеет место плоское напряженное состояние, то для расчета на прочность необходимо применить ту или иную теорию прочности. Главные напряжения имеют следующие значения:
т. е. проверка прочности ведется, как в случае одноосного напряженного состояния. По четвертой гипотезе прочности,
т. е. то же условие, что и по третьей гипотезе прочности. 2. Цилиндрический сосуд. В этом случае Из уравнения Лапласа получаем
Для определения напряжения Проецируя на ось сосуда все силы, действующие на отсеченную часть, получаем
где Таким образом,
Заметим, что в силу тонкостенности кольца, представляющего собой сечение цилиндра, по которому действуют напряжения
Условие прочности по третьей гипотезе прочности для цилиндрического сосуда
Условие прочности, по четвертой гипотезе прочности,
Пример. Определить толщину стенок цилиндрического резервуара для хранения жидкости с удельным весом g = 10 кН/м3; размеры резервуара показаны на рис. 8.3. Допускаемое напряжение для материала стенок
Рис. 8.3
Решение. Давление жидкости на стенки сосуда пропорционально расстоянию от свободной поверхности:
Если толщина стенки постоянна, то расчет ведется по наибольшему давлению у основания:
Толщина стенки:
|

 минимального радиуса кривизны стенки.
минимального радиуса кривизны стенки. и
и  .
. и
и  Нагрузка на элемент - внутреннее давление
Нагрузка на элемент - внутреннее давление  , нормальное к поверхности элемента.
, нормальное к поверхности элемента.
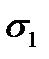 и
и  . Поскольку толщина стенок незначительна, как уже было отмечено, можно считать эти напряжения равномерно распределенными по толщине стенки.
. Поскольку толщина стенок незначительна, как уже было отмечено, можно считать эти напряжения равномерно распределенными по толщине стенки. . Проекция напряжения
. Проекция напряжения  на направление нормали представится отрезком аb, равным
на направление нормали представится отрезком аb, равным  Проекция усилия, действующего на грани 1-4 (и 2-3), равна
Проекция усилия, действующего на грани 1-4 (и 2-3), равна 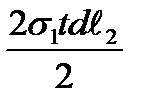 . Аналогично, проекция усилия, действующего по грани 1-2 (и 4-3), равна
. Аналогично, проекция усилия, действующего по грани 1-2 (и 4-3), равна  .
.

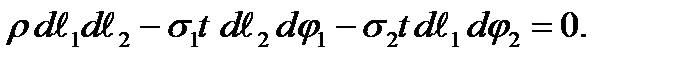
 и
и  имеем
имеем
 и разделив на t, получим
и разделив на t, получим (8.1)
(8.1)
 и
и  Из (8.1) следует
Из (8.1) следует  откуда
откуда (8.2)
(8.2) По третьей гипотезе прочности;
По третьей гипотезе прочности;  . Подставляя
. Подставляя  и
и  , получаем
, получаем (8.3)
(8.3) . Так как в данном случае
. Так как в данном случае  , то
, то (8.4)
(8.4) (радиус цилиндра) и
(радиус цилиндра) и  (радиус кривизны образующей цилиндра).
(радиус кривизны образующей цилиндра). откуда
откуда (8.5)
(8.5) рассечем сосуд плоскостью, перпендикулярной его оси, и рассмотрим условие равновесия одной из частей сосуда (рис. 47 б).
рассечем сосуд плоскостью, перпендикулярной его оси, и рассмотрим условие равновесия одной из частей сосуда (рис. 47 б). (8.6)
(8.6) - равнодействующая сил давления газа на днище сосуда.
- равнодействующая сил давления газа на днище сосуда. , откуда
, откуда (8.7)
(8.7) , площадь его подсчитана как произведение длины окружности на толщину стенки. Сравнивая
, площадь его подсчитана как произведение длины окружности на толщину стенки. Сравнивая 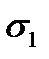 и
и  в цилиндрическом сосуде, видим, что
в цилиндрическом сосуде, видим, что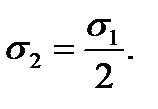
 (8.8)
(8.8) (8.9)
(8.9) = 100 МПа = 100.103 кПа.
= 100 МПа = 100.103 кПа.






