Кручение с изгибом. Брус, изображенный на рис
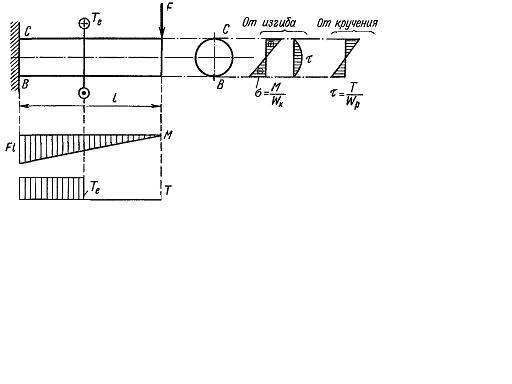
Брус, изображенный на рис. 7.5, работает на кручение и изгиб. В машиностроительных конструкциях детали, работающие на кручение и изгиб, встречаются очень часто. Характерным примером таких деталей являются валы различных машин. Начнем с того, что, пользуясь принципом независимости действия сил, определим отдельно напряжения, возникающие в брусе при кручении, и отдельно - при изгибе. При изгибе в поперечных сечениях бруса возникают нормальные напряжения, достигающие наибольшего значения в крайних волокнах балки: В случае, изображенном на рис. 7.5, сечение, где возникает наибольший изгибающий момент, совпадает с сечением, где возникает наибольший крутящий момент. Это сечение у заделки. В этом сечении (опасном) опасными являются точки С иВ. Рассмотрим напряженное состояние в точке С. Но площадке поперечного сечения, проходящего через эту точку, действуют наибольшие касательные напряжения от кручения
Рис. 7.5.
По площадке продольного сечения нормальные напряжения отсутствуют, а касательные (в силу закона парности) имеют то же значение, что и в поперечном сечении. Так как напряженное состояние двухосное, то для проверки прочности применяем одну из гипотез прочности. Имея в виду валы, изготовленные из стали, применяем третью или четвертую гипотезу прочности. Для этого необходимо определить главные напряжения для заданного напряжения состояния (рис. 7.6). Главные напряжения определяются по известной формуле
Рис. 7.6. Условие прочности - по третьей гипотезе (гипотеза наибольших касательных напряжений),
Подставляя сюда значения
Учитывая, что
Отсюда получим зависимость для подбора сечения (проектного расчета):
Напоминаем, что в случае, если вал испытывает изгиб в двух взаимно перпендикулярных плоскостях, то
По четвертой гипотезе прочности (гипотезе удельной потенциальной энергии изменения формы), условие прочности для случая плоского напряженного состояния имеет вид
Подставляя значения
но
Отсюда для подбора сечения
|

 и касательные напряжения, достигающие наибольшего значения у нейтральной оси. От кручения в поперечных сечениях возникают касательные напряжения, достигающие наибольшего значения в точках контура сечения;
и касательные напряжения, достигающие наибольшего значения у нейтральной оси. От кручения в поперечных сечениях возникают касательные напряжения, достигающие наибольшего значения в точках контура сечения; 
 и наибольшие (в данном случае растягивающие) нормальные напряжения от изгиба
и наибольшие (в данном случае растягивающие) нормальные напряжения от изгиба 
 (7.28)
(7.28)

 и
и  , получаем
, получаем (7.29)
(7.29)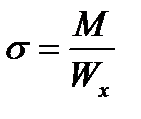 и
и  , получаем
, получаем (7.30)
(7.30) (7.31)
(7.31) (7.32)
(7.32) (7.33)
(7.33) и
и  , выраженные через
, выраженные через  и
и  в поперечном сечении вала, получаем
в поперечном сечении вала, получаем (7.34)
(7.34) и
и  , следовательно,
, следовательно, (7.35)
(7.35) (7.36)
(7.36)


