Формула Эйлера для критической силы. Рассмотрим, сжатый стержень в критическом состоянии, когда сжимающая сила достигла критического значения
Рассмотрим, сжатый стержень в критическом состоянии, когда сжимающая сила достигла критического значения, т. е. примем, что стержень слегка изогнут (рис. 9.3). Если моменты инерции относительно двух главных центральных осей поперечного сечения не равны между собой, то продольный изгиб произойдет в плоскости наименьшей жесткости, т. е. поперечные сечения стержня будут поворачиваться вокруг той оси, относительно которой момент инерции имеет минимальное значение. В этом легко убедиться, сжимая гибкую линейку. Для изучения продольного изгиба и определения критической силы используем приближенное дифференциальное уравнение изогнутой оси балки
Изгибающий момент относительно центра тяжести сечения в изогнутом состоянии
Рис. 9.3.
Рис. 9.3.
Знак минус берется потому, что стержень изгибается выпуклостью вверх, а прогиб
Обозначая
получаем
Это линейное дифференциальное уравнение второго порядка. Его общее решение, как известно из математики, имеет вид
Здесь С и D - постоянные интегрирования, для определения которых используем известные условия на концах стержня: 1) при z = 0, 2) при Из первого условия получим С =0. Следовательно, стержень изгибается по синусоиде 1-й случай. D =0. Но если С =0 и D =0, то, как следует из уравнения (9.5), прогибы стержня равны нулю, что противоречит исходной предпосылке. 2-й случай, sinα С практической точки зрения интерес представляет лишь наименьшее значение критической силы, при котором происходит потеря устойчивости стержня. Первый корень n =0 не дает решения задачи. При n =1 получаем наименьшее значение критической силы:
|

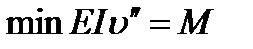 (9.2)
(9.2) (9.3)
(9.3)
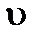 положителен. Если бы стержень изогнулся выпуклостью вниз, то момент был бы положительным, но прогибы
положителен. Если бы стержень изогнулся выпуклостью вниз, то момент был бы положительным, но прогибы 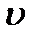 были бы отрицательными, и мы снова получили бы тот же результат.
были бы отрицательными, и мы снова получили бы тот же результат.

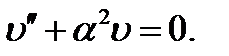 (9.4)
(9.4) (9.5)
(9.5) = 0;
= 0;
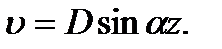 Из второго условия получим
Из второго условия получим  Это соотношение справедливо в двух случаях.
Это соотношение справедливо в двух случаях.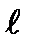 =0. Это условие выполняется, когда
=0. Это условие выполняется, когда  принимает следующий бесконечный ряд значений:
принимает следующий бесконечный ряд значений:  , где n - любое целое число. Отсюда
, где n - любое целое число. Отсюда  , а так как
, а так как 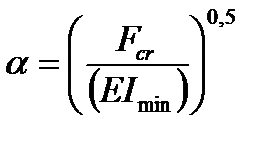 , тo
, тo  . Таким образом, получается бесчисленное множество значений критических сил, соответствующих различным формам искривления стержня.
. Таким образом, получается бесчисленное множество значений критических сил, соответствующих различным формам искривления стержня. (9.6)
(9.6)


