Реализация задания на компьютере с помощью ППП Ехсеl. Здесь так же, как и в парной регрессии необходимо выполнить задание в двух вариантах:
Здесь так же, как и в парной регрессии необходимо выполнить задание в двух вариантах: ВНИМАНИЕ! Каждый студент должен выполнить индивидуальное задание с использованием компьютера в двух вариантах: 3) Реализовать формулы (2.1) – (2.19) с помощью одиночных функций ППП Ехсеl. 4) Использовать «комплексные» функции, выходом которых являются не только коэффициенты регрессии, но и дополнительная регрессионная статистика (среднеквадратические отклонения, коэффициент детерминации и т.д.). 3) Реализация регрессионных формул (2.1) – (2.19) с помощью одиночных функций. В первую очередь необходимо представить данные наблюдений в матричной форме (см. рис.2.1). Затем используя матричные функции из Мастер функций: МОБР, МУМНОЖ, ТРАНСП реализуем формулу (2.8), результатом которой будет вектор оценок коэффициентов регрессии В. Примечание. Вышеперечисленные функции должны быть введены, как функции массивов в интервал с необходимым количеством строк и столбцов (см. реализацию функции ЛИНЕЙН в парной регрессии). Для вычисления дисперсий Проверка соответствия предпосылкам МНК осуществляется по критерию Дарбина – Уотсона. Критические значения распределения определяются из таблицы (электронного варианта таблицы нет). Примерный вид реализации задачи на компьютере представлен на рис.2.2.
Рис.2.1
Рис.2.2 Для графической иллюстрации приближения корреляционной функции
Рис.2.3
На рис.2.2 в ячейке с названием «S(Yp)» была вычислена стандартная ошибка прогноза объясняемой переменной по формуле: S (Yр) = S которую необходимо использовать для определения интервальной оценки среднего значения предсказания.
4) Использование «Комплексных» функций. В качестве такой функции может быть использована встроенная статистическая функция ЛИНЕЙН. Дополнительная регрессионная статистика (в случае ее инициализации) будет выводиться в порядке, указанном на рис.2.4.
Рис.2.4. Обозначения на рисунке следующие: b – свободный коэффициент линейной регрессии; mi – коэффициенты при хi; Se – стандартные ошибки коэффициентов регрессии; r2 - коэффициент детерминации; Sey - стандартная ошибка для оценки у; F – F - статистика; df – количество степеней свободы; Ssрег – регрессионная сумма квадратов; Ssост – остаточная сумма квадратов. Для лучшей наглядности можно нужные значения из этой таблицы выбирать индивидуально и размещать в нужных форматах документа. Для этого можно воспользоваться функцией ИНДЕКС из категории Ссылки и массивы. Выделите ячейку, в которую хотите поместить отдельный элемент массива и введите формулу, например: Индекс (Линейн (Y; Х; 1; 1); 1; 2). В результате в данную ячейку будет записан элемент (1, 2) регрессионной таблицы. Таким образом, можно создать более наглядную таблицу. Пример решения задания на компьютере с использованием функции ЛИНЕЙН представлен на рисунках 2.5, 2.6.
Рис.2.5
Рис.2.6
Так же, как и в парной регрессии для оценки коэффициентов множественной регрессии и получения дополнительной статистики кроме функции Линейн можно воспользоваться Статистическим пакетом анализа данных. Установка пакета анализа достаточно подробно описана в п. 1.2. В диалоговом окне Анализ данных в списке Инструменты анализа выберите строку Регрессия и заполните диалоговое окно ввода данных и параметров вывода. Результаты регрессионного анализа для данных выше использованного примерапредставлены на рис.2.7.
Рис.2.7
2.3. Контрольные задания
Задача 1. Предполагается, что объем Q предложения некоторого блага для функционирующей в условиях конкуренции фирмы зависит линейно от цены Р данного блага и заработной платы W сотрудников фирмы, производящих данное благо: Q =
Статистические данные, собранные за 12 месяцев, занесены в таблицу.
Задание.
1. По МНК оценить коэффициенты линейной регрессии 2. Оценить статистическую значимость найденных эмпирических коэффициентов регрессии b i, i =0, 1, 2; 3. В соответствие с заданным значением 4. Вычислить коэффициент детерминации R 2 и оценить его статистическую значимость при заданном значении 5. Определить какой процент разброса зависимой переменной объясняется данной регрессией; 6. Сравнить коэффициент детерминации R 2 со скорректированным коэффициентом детерминации; 7. Вычислить статистику DW Дарбина-Уотсона и оценить наличие автокорреляции; 8. Посредством коэффициентов bi, i = 1, 2, оценить в % отношении влияние объясняющих переменных P и W на изменение объясняемой переменной; 9. Спрогнозировать значение объясняемой переменной Q прогн для прогнозных значений Р прогн, W прогн и определить доверительный интервал для Q прогн; 10. Сделать обобщающие выводы по регрессионной модели.
Вариант 1.1
Р прогн = 60, W прогн = 2,
Вариант 1.2
Р прогн = 75, W прогн = 1,
Вариант 1.3
Р прогн = 53, W прогн = 4,
Вариант 1.4
Р прогн = 28, W прогн = 9,
Вариант 1.5
Р прогн = 25, W прогн = 12,
Задача 2. Для объяснения изменения ВНП за 10 лет строится регрессионная модель с объясняющими переменными – потреблением (С) и инвестициями (I): ВНП =
Статистические данные приведены в таблице.
Задание. 1. По МНК оценить коэффициенты линейной регрессии 2. Оценить статистическую значимость найденных эмпирических коэффициентов регрессии bi, i =0, 1, 2; 3. В соответствие с заданным значением 4. Вычислить коэффициент детерминации R 2 и оценить его статистическую значимость при заданном значении 5. Определить какой процент разброса зависимой переменной объясняется данной регрессией; 6. Сравнить коэффициент детерминации R 2 со скорректированным коэффициентом детерминации; 7. Вычислить статистику DW Дарбина-Уотсона и оценить наличие автокорреляции; 8. Посредством коэффициентов bi, i = 1, 2, оценить в % отношении влияние объясняющих переменных С и I на изменение объясняемой переменной; 9. Спрогнозировать значение объясняемой переменной ВНП прогн для прогнозных значений С прогн, I прогн и определить доверительный интервал для ВНПпрогн; 10. Сделать обобщающие выводы по регрессионной модели. Вариант 2.1
С прогн = 20, I прогн = 4,
Вариант 2.2
С прогн = 20, I прогн = 4,
Вариант 2.3
С прогн = 14, 5, I прогн = 3,
Вариант 2.4
С прогн = 18, 0, I прогн = 3, 2,
Вариант 2.5
С прогн = 19, 0, I прогн = 4, 0, Задача 3. В таблице даны статистические данные о расходах на питание Y, душевом доходе Х1 и размере семьи Х2 для девяти групп семей. Построить регрессионную модель: Y =
Задание.
1. По МНК оценить коэффициенты линейной регрессии 2. Оценить статистическую значимость найденных эмпирических коэффициентов регрессии bi, i =0, 1, 2. 3. В соответствие с заданным значением 4. Вычислить коэффициент детерминации R 2 и оценить его статистическую значимость при заданном значении 5. Определить какой процент разброса зависимой переменной объясняется данной регрессией; 6. Сравнить коэффициент детерминации R 2 со скорректированным коэффициентом детерминации; 7. Вычислить статистику DW Дарбина-Уотсона и оценить наличие автокорреляции; 8. Посредством коэффициентов bi, i = 1, 2, оценить в % отношении влияние объясняющих переменных Х 1 и Х 2 на изменение объясняемой переменной; 9. Спрогнозировать значение объясняемой переменной Yпрогн для прогнозных значений Х 1 прогн, Х 2 прогн и определить доверительный интервал для Y прогн; 10. Сделать обобщающие выводы по регрессионной модели.
Вариант 3.1
Х 1 прогн = 8000, Х 2 прогн = 4, 0,
Вариант 3.2
Х 1 прогн = 10000, Х 2 прогн =3, 0,
Вариант 3.3
Х 1 прогн = 8000, Х 2 прогн =3, 0,
Вариант 3.4
Х 1 прогн = 13000, Х 2 прогн =3, 2,
Вариант 3.5
Х 1 прогн = 11000, Х 2 прогн =3, 0,
Задача 4. Изучается влияние стоимости основных и оборотных средств на величину валового дохода торговых предприятий. Для этого по 12 торговым предприятиям были получены данные приведенные в таблице. Построить регрессионную модель: Y = Задание. 1. По МНК оценить коэффициенты линейной регрессии 2. Оценить статистическую значимость найденных эмпирических коэффициентов регрессии bi, i =0, 1, 2. 3. В соответствие с заданным значением 4. Вычислить коэффициент детерминации R 2 и оценить его статистическую значимость при заданном значении 5. Определить какой процент разброса зависимой переменной объясняется данной регрессией; 6. Сравнить коэффициент детерминации R 2 со скорректированным коэффициентом детерминации; 7. Вычислить статистику DW Дарбина-Уотсона и оценить наличие автокорреляции; 8. Посредством коэффициентов bi, i = 1, 2, оценить в % отношении влияние объясняющих переменных Х 1 и Х 2 на изменение объясняемой переменной; 9. Спрогнозировать значение объясняемой переменной Y прогн для прогнозных значений Х 1 прогн, Х 2 прогн и определить доверительный интервал для Y прогн; 10. Сделать обобщающие выводы по регрессионной модели.
Вариант 4.1
Х 1 прогн = 140, Х 2 прогн =58,
Вариант 4.2
Х 1 прогн = 150, Х 2 прогн =100,
Вариант 4.3
Х 1 прогн = 100, Х 2 прогн =80,
Вариант 4.4
Х 1 прогн = 90, Х 2 прогн =50,
Вариант 4.5
Х 1 прогн = 50, Х 2 прогн =60,
Задача 5. Имеются данные по странам за 2005 год. Построить регрессионную модель: Y = Задание. 1. По МНК оценить коэффициенты линейной регрессии 2. Оценить статистическую значимость найденных эмпирических коэффициентов регрессии bi, i =0, 1, 2. 3. В соответствие с заданным значением 4. Вычислить коэффициент детерминации R 2 и оценить его статистическую значимость при заданном значении 5. Определить какой процент разброса зависимой переменной объясняется данной регрессией; 6. Сравнить коэффициент детерминации R2 со скорректированным коэффициентом детерминации; 7. Вычислить статистику DW Дарбина-Уотсона и оценить наличие автокорреляции; 8. Посредством коэффициентов bi, i = 1, 2, оценить в % отношении влияние объясняющих переменных Х 1 и Х 2 на изменение объясняемой переменной; 9. Спрогнозировать значение объясняемой переменной Y прогн для прогнозных значений Х 1 прогн, Х 2 прогн и определить доверительный интервал для Y прогн; 10. Сделать обобщающие выводы по регрессионной модели.
Вариант 5.1
Х 1 прогн = 80, Х 2 прогн =3500,
Вариант 5.2
Х 1 прогн = 75, Х 2 прогн =3000,
Вариант 5.3
Х 1 прогн = 72, Х 2 прогн =3500,
Вариант 5.4
|

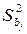 необходимо вычислить S 2 в соответствие с формулой (2.10). На основании Т -статистик делается вывод о значимости коэффициентов регрессии их доверительные интервалы. Значения tкр можно получить, используя статистическую функцию СТЬЮДРАСПОБР. По соответствующим формулам вычисляются коэффициент детерминации R 2 и F – критерий, на основании которых делается вывод о значимости уравнения регрессии в целом. Для нахождения критической точки fкр нужно воспользоваться функцией FРАСПОБР.
необходимо вычислить S 2 в соответствие с формулой (2.10). На основании Т -статистик делается вывод о значимости коэффициентов регрессии их доверительные интервалы. Значения tкр можно получить, используя статистическую функцию СТЬЮДРАСПОБР. По соответствующим формулам вычисляются коэффициент детерминации R 2 и F – критерий, на основании которых делается вывод о значимости уравнения регрессии в целом. Для нахождения критической точки fкр нужно воспользоваться функцией FРАСПОБР.
 и выборочных данных yi воспользуемся Мастером диаграмм (График) (см. рис.2.3).
и выборочных данных yi воспользуемся Мастером диаграмм (График) (см. рис.2.3).
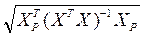 ,
,


 0 +
0 +  .
. построить доверительные интервалы для найденных коэффициентов;
построить доверительные интервалы для найденных коэффициентов;


