Реализация задания на компьютере с помощью ППП Excel
В качестве заданий по этой теме используется статистический материал, представленный в теме «Парная регрессия». Предлагается каждому студенту попробовать описать функционально связь между экономическими показателями не только линейной функцией (что было сделано в первой части задания), но и рядом нелинейных моделей, а именно:
1. Полиномом второго порядка
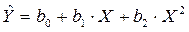 ; ;
2. Степенной функцией
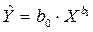 ; ;
3. Показательной функцией
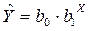 ; ;
4. Равносторонней гиперболой
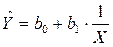 . .
По результатам оценивания моделей выбирается наилучшая модель с точки зрения достоверности статистическим данным.
Для оценивания показательной модели можно использовать стандартную функцию ЛГРФПРИБЛ (смотри приложение «Стандартные функции»). Эта функция, как и функция ЛИНЕЙН возвращает статистику по регрессии. Порядок регрессионной статистики в выходном массиве такой же, как у ЛИНЕЙН (рис. 3.1)
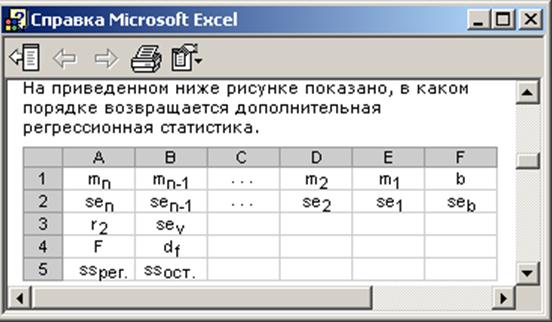
Рис.3.1.
Для оценивания остальных моделей необходимо использовать функцию ЛИНЕЙН.
Пример решения задания на компьютере представлен ниже.
Имеется информация по однотипным предприятиям торговли о сроках эксплуатации типового оборудования и затратах на его ремонт:
| № предприятия
|
|
|
|
|
|
|
|
|
|
| | Срок эксплуатации (лет)
|
|
|
|
|
|
|
|
|
|
| | Затраты (тыс. руб.)
| 1, 5
| 2, 0
| 1, 4
| 2, 3
| 2, 7
| 4, 0
| 2, 3
| 2, 5
| 6, 6
| 1, 7
| В целях нормирования расходования средств необходимо подобрать наиболее адекватную статистическим данным экономико-математическую модель из следующих функций:
1) Линейной;
2) Полином 2-го порядка;
3) Степенной;
4) Показательной;
5) Равносторонней гиперболы;
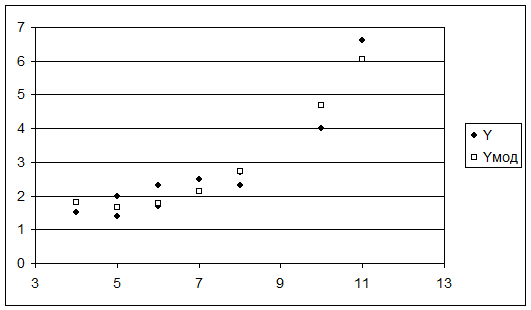
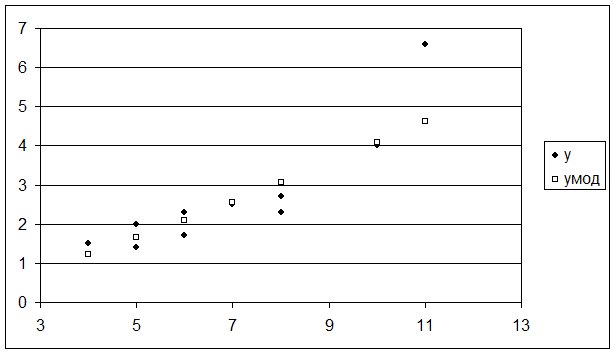
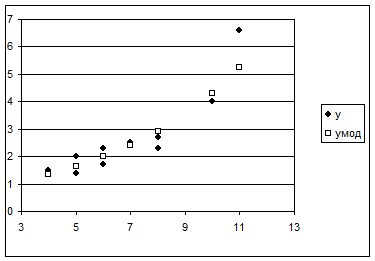
Результаты решения этой задачи с использованием ППП Ехсеl представлены на рисунках 3.2 - 3.6.
| 1. Y = b0 + b1*X
|
|
| | |
|
|
|
| | | х
| у
| умод
| е
| Tb1
| Tb0
| Rкв
| |
| 1, 5
| 0, 867391
| 0, 6326087
| 5, 3969895
| -1, 9019578
| 0, 78452627
| |
|
| 1, 478261
| 0, 5217391
|
|
|
| |
| 1, 4
| 1, 478261
| -0, 078261
| F
| Ср.ош А, %
| Прогн, V, %
| |
| 2, 3
| 2, 08913
| 0, 2108696
| 29, 127496
| 21, 5868577
| 28, 4323048
| |
| 2, 7
| 3, 31087
| -0, 61087
| | |
|
| 4, 532609
| -0, 532609
| | |
| 2, 3
| 3, 31087
| -1, 01087
| | |
| 2, 5
| 2, 7
| -0, 2
| | |
| 6, 6
| 5, 143478
| 1, 4565217
| | |
| 1, 7
| 2, 08913
| -0, 38913
| | |
|
|
|
| | | Статист. Лин.
|
|
| | | 0, 61087
| -1, 57609
|
|
| | | 0, 113187
| 0, 828666
|
|
| | | 0, 784526
| 0, 767672
|
|
| | | 29, 1275
|
|
|
| | | 17, 16543
| 4, 714565
| 
|
| |
| Al = 0, 1
| | Fкр
| Ткр
| | 3, 45791307
| 2, 3060056
|
Рис. 3.2

| 2. Y = b0 + b1*X + b2*X^2
| X1=x
|
| | |
|
|
|
|
| | | X1
| X2
| Y
| Yмод
| е
| | |
|
| 1, 5
| 1, 8141436
| -0, 3141436
| Tb2
| Tb1
| Tb0
| Rкв
| | |
|
|
| 1, 6652062
| 0, 3347938
| 3, 564425
| -2, 39118
| 2, 593683
| 0, 923455
| | |
|
| 1, 4
| 1, 6652062
| -0, 2652062
| | |
|
| 2, 3
| 1, 7677157
| 0, 5322843
| F
| Ср.ош А, %
| Прогн, V, %
| |
|
| 2, 7
| 2, 7270754
| -0, 0270754
| 42, 225118
| 14, 40654772
| 18, 1162156
| | |
|
|
| 4, 6922228
| -0, 6922228
| | |
|
| 2, 3
| 2, 7270754
| -0, 4270754
| | |
|
| 2, 5
| 2, 1216721
| 0, 3783279
| | |
|
| 6, 6
| 6, 0519669
| 0, 5480331
| | |
|
| 1, 7
| 1, 7677157
| -0, 0677157
| | |
|
|
|
|
| | | Статист. Лин.
|
| | | 0, 125723
| -1, 28045
| 4, 924362
| | | 0, 035272
| 0, 535488
| 1, 898598
| | | 0, 923456
| 0, 489138
| #Н/Д
| | | 42, 22512
|
| #Н/Д
| | | 20, 20521
| 1, 674791
| 
| | | | | | | | | | | | | | | | | |
Рис. 3.3
| | | |  |
| 3. Y = b0*x^b1
| Y = lny
| B0 = lnb0
| X = lnx
|
|
|
| |
|
|
|
|
|
|
|
| | х
| у
| Y
| X
| Yмод
| умод
| Е
| е
| |
| 1, 5
| 0, 405465
| 1, 3862944
| 0, 2115272
| 1, 235564
| 0, 193938
| 0, 2644364
| |
|
| 0, 693147
| 1, 6094379
| 0, 5028681
| 1, 653457
| 0, 190279
| 0, 3465433
| |
| 1, 4
| 0, 336472
| 1, 6094379
| 0, 5028681
| 1, 653457
| -0, 1664
| -0, 2534567
| |
| 2, 3
| 0, 832909
| 1, 7917595
| 0, 7409109
| 2, 097846
| 0, 091998
| 0, 2021544
| |
| 2, 7
| 0, 993252
| 2, 0794415
| 1, 1165146
| 3, 054191
| -0, 12326
| -0, 3541906
| |
|
| 1, 386294
| 2, 3025851
| 1, 4078555
| 4, 087181
| -0, 02156
| -0, 0871809
| |
| 2, 3
| 0, 832909
| 2, 0794415
| 1, 1165146
| 3, 054191
| -0, 28361
| -0, 7541906
| |
| 2, 5
| 0, 916291
| 1, 9459101
| 0, 9421732
| 2, 565551
| -0, 02588
| -0, 0655509
| |
| 6, 6
| 1, 88707
| 2, 3978953
| 1, 5322944
| 4, 628785
| 0, 354775
| 1, 971215
| |
| 1, 7
| 0, 530628
| 1, 7917595
| 0, 7409109
| 2, 097846
| -0, 21028
| -0, 3978456
| |
|
|
|
|
|
| СумЕкв
| Сумeкв
| | Статист. Лин.
|
|
|
|
| 0, 376814
| 5, 0452469
| | 1, 305621
| -1, 59845
|
| b0
| b1
| Tb1
| Tb0
| Rкв
| F
| | 0, 224728
| 0, 432331
|
| 0, 2022102
| 1, 3056208
| 5, 809771
| -3, 6972812
| 0, 769412
| 26, 69404
| | 0, 808399
| 0, 217029
|
|
|
| | | 33, 75344
|
|
| 5, 0452469
| 
| Ср.ош А, %
| Прогн, V, %
| Sкв
| | 1, 589847
| 0, 376814
|
|
|
| 16, 58298291
| 29, 4125349
| 0, 6306559
| | | | | | | | | | | | |
Рис. 3.4
| | | |  |
| 4. Y=b0*b1^x c использованием стандартной функции ЛГРФПРИБЛ
| | | х
| у
| lny
| lnумод
| умод
| еln
| е
| | |
| 1, 5
| 0, 405465
| 0, 3013904
| 1, 351737
| 0, 104075
| 0, 148263
| | |
|
| 0, 693147
| 0, 4947415
| 1, 6400743
| 0, 198406
| 0, 359926
| | |
| 1, 4
| 0, 336472
| 0, 4947415
| 1, 6400743
| -0, 15827
| -0, 24007
| | |
| 2, 3
| 0, 832909
| 0, 6880926
| 1, 9899164
| 0, 144816
| 0, 310084
| | |
| 2, 7
| 0, 993252
| 1, 0747949
| 2, 9293919
| -0, 08154
| -0, 22939
| | |
|
| 1, 386294
| 1, 4614971
| 4, 3124107
| -0, 0752
| -0, 31241
| | |
| 2, 3
| 0, 832909
| 1, 0747949
| 2, 9293919
| -0, 24189
| -0, 62939
| | |
| 2, 5
| 0, 916291
| 0, 8814438
| 2, 414383
| 0, 034847
| 0, 085617
| | |
| 6, 6
| 1, 88707
| 1, 6548482
| 5, 2322856
| 0, 232221
| 1, 367714
| | |
| 1, 7
| 0, 530628
| 0, 6880926
| 1, 9899164
| -0, 15746
| -0, 28992
| | | Статист. Нелин.
|
|
|
|
|
| | 1, 213309
| 0, 246967
|
|
|
|
|
| | 0, 025906
| 0, 189661
|
|
|
|
|
| | 0, 874423
| 0, 175701
|
|
|
| Sкв(ln)
| Sкв
| | 0, 0308709
| 0, 35171198
| | S(ln)
| S
| | 0, 1757011
| 0, 5930531
| | Sb1(ln)
| Sb1
| | 0, 0259057
| 0, 08744091
| | Sb0(ln)
| Sb0
| | 0, 1896609
| 0, 40982091
| | Tb1(ln)
| Tb1
| | 7, 4636488
| 13, 8757561
| | Tb0(ln)
| Tb0
| | -2, 4887256
| 1, 52199351
| | Rкв(ln)
| Rкв
| | 0, 8744232
| 0, 8714033
| | R(ln)
| R
| | 0, 935106
| 0, 93348985
| | Rxy(ln)
| Rxy
| | 0, 935106
| 0, 88573488
| | F(ln)
| F
| | 55, 706053
| 54, 2099939
|
| |
| | | 55, 70605
|
|
|
|
| | | 1, 719694
| 0, 246967
|
| 2, 813696
| 
| | | | | | | | | | | | | | | | | | | | | | |
|
| | Ср.ош А, %
| Прогн, V, %
| | 14, 338321
| 21, 96493
|
| |
Рис. 3.5
| 5. Y = b0 + b1*1/x
|
| X = 1/x
|
| |
|
|
|
|
| | х
| у
| X
| Yмод
| е
| |
| 1, 5
| 0, 25
| 0, 5035001
| 0, 9964999
| |
|
| 0, 2
| 1, 6807425
| 0, 3192575
| |
| 1, 4
| 0, 2
| 1, 6807425
| -0, 2807425
| |
| 2, 3
| 0, 166667
| 2, 4655708
| -0, 1655708
| |
| 2, 7
| 0, 125
| 3, 4466061
| -0, 7466061
| |
|
| 0, 1
| 4, 0352273
| -0, 0352273
| |
| 2, 3
| 0, 125
| 3, 4466061
| -1, 1466061
| |
| 2, 5
| 0, 142857
| 3, 0261624
| -0, 5261624
| |
| 6, 6
| 0, 090909
| 4, 2492714
| 2, 3507286
| |
| 1, 7
| 0, 166667
| 2, 4655708
| -0, 7655708
| | Статист. Лин.
| | | -23, 5448
| | Tb1
| Tb0
| Rкв
| F
| Ср.ош А, %
| Прогн, V, %
| | -3, 239832
| 5, 3710378
| 0, 567486
| 10, 49651
| 28, 973034
| 40, 282365
|
| | 6, 389712
| | | 7, 267305
| 1, 189661
| | | 0, 567486
| 1, 087624
| | | 10, 49651
|
| | | 12, 41659
| 9, 463405
| | 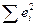
Рис. 3.6
Поясним некоторые обозначения, используемые на рисунках:
- параметры с индексами «мод» (Yмод, …) означают модельные (оценки) значения этих параметров;
- «ln» - логарифмы соответствующих переменных;
- «Статист.лин.» - результаты использования функции ЛИНЕЙН;
- «Статист.нелин.» - результаты использования функции ЛГРФПРИБЛ;
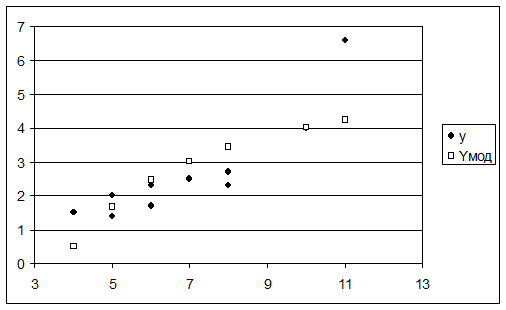
- «Ср.Ош.А» - относительная ошибка аппроксимации в процентах, вычисляемая по формуле: 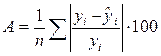 ; ;
- «Прогн.V» - относительная ошибка прогноза в процентах, реализуемая соотношением:  , где S – стандартная ошибка регрессии; , где S – стандартная ошибка регрессии;  - среднее значение Y. - среднее значение Y.
Параметры A и V используются для выбора «наилучшей» модели аппроксимации в случае примерного равенства основных критериев качества уравнений регрессии.
Результатом выполнения данного задания является выбор наиболее адекватной статистическим данным математической модели. В выводах должны быть приведены статистические критерии, обосновывающие данный выбор.
Вопросы для подготовки к защите индивидуального задания
1. Приведите примеры нелинейных моделей, используемых в эконометрике.
2. Какие из известных вам типов нелинейных моделей поддаются непосредственной линеаризации?
3. Как линеаризуются модели гиперболического вида?
4. Как линеаризуются модели экспоненциального вида?
5. Как линеаризуются модели степенного вида?
6. Как линеаризуются модели логарифмического вида?
7. Каковы признаки качественной регрессионной модели?
8. Назовите основные виды ошибок спецификации.
9. Как можно обнаружить ошибки спецификации?
10. Можно ли обнаружить ошибки спецификации с помощью исследования остаточного члена?
11. В чем суть теста Рамсея?

Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
|

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при которых тело находится под действием заданной системы сил...
|

Теория усилителей. Схема Основная масса современных аналоговых и аналого-цифровых электронных устройств выполняется на специализированных микросхемах...
|

Логические цифровые микросхемы Более сложные элементы цифровой схемотехники (триггеры, мультиплексоры, декодеры и т.д.) не имеют...
|
Основные разделы работы участкового врача-педиатра Ведущей фигурой в организации внебольничной помощи детям является участковый врач-педиатр детской городской поликлиники...
Ученые, внесшие большой вклад в развитие науки биологии Краткая история развития биологии. Чарльз Дарвин (1809 -1882)- основной труд « О происхождении видов путем естественного отбора или Сохранение благоприятствующих пород в борьбе за жизнь»...
Этапы трансляции и их характеристика Трансляция (от лат. translatio — перевод) — процесс синтеза белка из аминокислот на матрице информационной (матричной) РНК (иРНК...
|
Принципы и методы управления в таможенных органах Под принципами управления понимаются идеи, правила, основные положения и нормы поведения, которыми руководствуются общие, частные и организационно-технологические принципы...
ПРОФЕССИОНАЛЬНОЕ САМОВОСПИТАНИЕ И САМООБРАЗОВАНИЕ ПЕДАГОГА Воспитывать сегодня подрастающее поколение на современном уровне требований общества нельзя без постоянного обновления и обогащения своего профессионального педагогического потенциала...
Эффективность управления. Общие понятия о сущности и критериях эффективности. Эффективность управления – это экономическая категория, отражающая вклад управленческой деятельности в конечный результат работы организации...
|
|

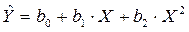 ;
;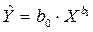 ;
;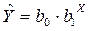 ;
;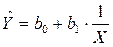 .
.






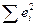
 ;
; , где S – стандартная ошибка регрессии;
, где S – стандартная ошибка регрессии;  - среднее значение Y.
- среднее значение Y.


