Реализация задания на компьютере с помощью ППП Ехсеl

 

С целью повышения эффективности решения задачи необходимо воспользоваться возможностями ППП Ехсеl. Для этого требуется инициировать опцию Мастер функций. В основном будет востребована категория Статистические и некоторые функции из категорий Математические и Ссылки и массивы. Перечень этих функций и краткое описание представлены в Приложении «Стандартные функции».

ВНИМАНИЕ! Каждый студент должен выполнить индивидуальное задание с использованием компьютера в двух вариантах:

1) Реализовать формулы (1.1) – (1.15) с помощью ППП Ехсеl.

2) Использовать «комплексные» функции, выходом которых являются не только коэффициенты регрессии, но и дополнительная регрессионная статистика (среднеквадратические отклонения, коэффициент детерминации и т.д.).

1) Реализация регрессионных формул (1.1) – (1.15).

В начале необходимо воспользоваться Мастером диаграмм, выбрать тип Точечная и нанести значения выборки на корреляционное поле (рис. 1.1). По расположению точек на графике сделать предварительный анализ о возможной линейной зависимости между переменными.

С помощью функций ППП Ехсеl определить оценки коэффициентов регрессии b ₀, b ₁, реализуя формулы (1.7), (1.8), например , вычисляются с помощью функции СРЗНАЧ, а с помощью функции СУММПРОИЗВ()/ n. Для вычисления можно воспользоваться соотношением СУММКВ(число1; число2;...) / n. Однако составляющие коэффициента b ₁ можно вычислить проще, через Статистические функции КОВАР(массив1; массив2) Cov (X, Y) и ДИСПР S_x ² или СТАНДОТКЛОНП S_x ².

По соответствующим формулам вычисляются дисперсии , и на основании Т -статистик делается вывод о значимости коэффициентов регрессии и определяются их доверительные интервалы. Значения t_кр можно получить, используя статистическую функцию СТЬЮДРАСПОБР.

 

Рис. 1.1.

 

 

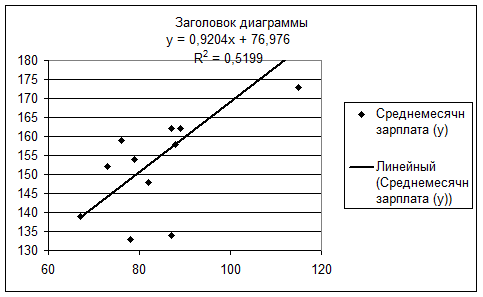
Примерный вид реализации задачи на компьютере представлен на рис.1.2.

Для графической иллюстрации приближения корреляционной функции и выборочных данных y_i воспользуемся Мастером диаграмм (Точечная) (см. рис.1.3.).

Параметры линейной регрессии можно рассчитать и сразу. Для этого в Ехсеl существуют функции Наклон и Отрезок. Функция Наклон служит для определения углового коэффициента связи (b ₁), а функция Отрезок – для определения свободного члена уравнения (b ₀). В качестве аргументов этих функций вводятся массивы Х и Y.

Кроме перечисленных возможностей существует еще и следующая возможность. Построим график по имеющимся данным. Чтобы ось Х отражала фактические данные, выберем тип диаграммы Точечная. На построенной диаграмме выделим график функции, щелкнув по ней левой кнопкой мыши. Затем нажмем правую кнопку мыши, выведем контекстное зависимое меню, в котором выберем опцию Добавить линию тренда. В панели линии тренда во вкладке Тип надо выбрать тип функции (по умолчанию выбирается Линейная). Во вкладке Параметры введем название тренда (теоретической кривой) и установим флажки «Показывать уравнение на диаграмме» и «Поместить на диаграмму величину достоверности аппроксимации (R^2)». В результате появится график вида (рис.1.4.).

		Парная регрессия(пример)
		y = b0 + b1*x
Введите исходную информацию
Территория	Прожиточный	Среднемесячн	Оценка У	Ошибки Е
региона	минимум (х)	зарплата (у)
			148, 7700683	-15, 77006831
			152, 4517905	-4, 45179052
			157, 0539433	-23, 05394328
			149, 6904989	4, 309501138
			158, 8948044	3, 105195612
			174, 5421238	20, 45787622
			138, 6453322	0, 354667771
			157, 9743738	0, 025626164
			144, 1679155	7, 832084455
			157, 0539433	4, 946056717
			146, 9292072	12, 0707928
			182, 8259988	-9, 825998758
Вычисление по формулам		Al
				0, 05
Вспомогательные параметры			Кэфф. регрессии
Хср	Уср	ХУср	ХквСр		В0	В1
85, 58333333	155, 75		7492, 25		76, 9764852	0, 92043055
КвХср	ЕквСр	УквСр	КвУср		Кху	Rкв
7324, 506944	131, 2435245	24531, 41667	24258, 0625		0, 72102521	0, 51987736
Тв1	Тв0	Ткр	Sb0Кв	Sb1Кв	SКв
3, 290594434	3, 179327594	2, 433444024	586, 1997046	0, 078240809	157, 492229

 

 

Рис.1.2.

 

 

Рис.1.3.

 

Рис.1.4.

 

2) Использование «Комплексных» функций.

Одной из таких функций является встроенная статистическая функция ЛИНЕЙН (описание функции и ее аргументов приведено в приложении «Стандартные функции»).

Дополнительная регрессионная статистика (в случае ее инициализации) будет выводиться в порядке, указанном в следующей схеме:

 

Значение коэффициента b1	Значение коэффициента b0
Среднеквадратическое отклонение b1	Среднеквадратическое отклонение b0
Коэффициент детерминации R2	Среднеквадратическое отклонение у
F - статистика	Число степеней свободы
Регрессионная сумма квадратов	Остаточная сумма квадратов

 

Для данных из вышерассмотренного примера результат вычисления функции ЛИНЕЙН представлен на рис.1.5.

 

Территория	Прожиточный	Среднемесячн
региона	минимум (х)	зарплата (у)		0, 920431	76, 97649
				0, 279716	24, 21156
				0, 519877	12, 54959
				10, 82801
				1705, 328	1574, 922

Рис.1.5.

Примечание. Функция ЛИНЕЙН должна быть введена, как формула массива в интервал с необходимым количеством строк и столбцов. Перед использованием функции ЛИНЕЙН выделяем ячейку (1, 1) (1-ая строка, 1-ый столбец) массива, в который будет занесен результат вычисления функции, затем инициализируем Мастер функций, выбираем категорию Статистические и функцию Линейн. Щелкните по кнопке ОК. После заполнения аргументов в ячейке (1, 1) появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, выделите массив нужной размерности, включая и ячейку (1, 1) (в нашем примере 5 – строк, 2 – столбца), нажмите на клавишу < F2>, а затем – на комбинацию клавиш < CTRL> +< SHIFT> +< ENTER>.

Для лучшей наглядности можно нужные значения из этой таблицы выбирать индивидуально и размещать в нужных форматах документа. Для этого можно воспользоваться функцией ИНДЕКС из категории Ссылки и массивы. Выделите ячейку, в которую хотите поместить отдельный элемент массива и введите формулу, например: Индекс (Линейн (Y; Х; Истина; Истина); 1; 2).

В результате в данную ячейку будет записан элемент (1, 2) регрессионной таблицы, т.е. значение b ₀. Таким образом можно создать более наглядную таблицу (рис.1.6)

	b0 b1 Sb0 Sb1             76, 97649 0, 920431 24, 21156 0, 279716                           Sy r2 F -статист Кол.ст.св Ss рег Ss ост             12, 54959 0, 519877 10, 82801   1705, 328 1574, 922

 

 

 

 

Рис.1.6.

 

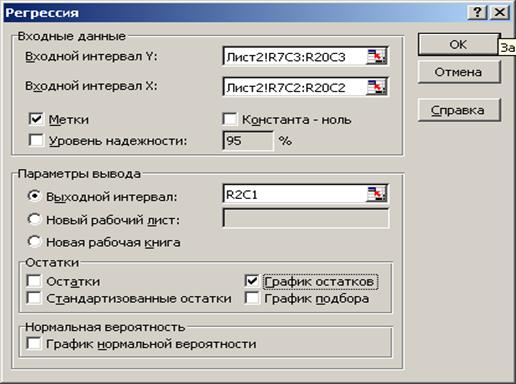
Кроме функции Линейн можно также воспользоваться Статистическим пакетом анализа данных. Чтобы установить пакет Анализа данных в меню Сервис, выберите команду Надстройки и установите флажок Пакет анализа. Диалоговое окно данной опции приведено на рис.1.7.

Чтобы запустить пакет анализа в меню Сервис, выберите команду Анализ данных. В диалоговом окне Анализ данных в списке Инструменты анализа выберите строку Регрессия (рис.1.8).

Примечание. В Ехсеl-2007 установка пакета осуществляется по схеме: «Officе» Параметры Ехсеl Неактивные надстройки приложений Пакет анализа в окне Надстройки (рис.1.7) установить флажок Пакет анализа ОК. Запускается пакет анализа в меню Данные.

Заполните диалоговое окно ввода данных и параметров вывода (рис.1.9):

Входной интервал Y – диапазон, содержащий данные объясняемой переменной;

Входной интервал Х – диапазон, содержащий данные объясняющей переменной;

Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;

Константа – ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;

Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;

Новый рабочий лист – можно задать произвольное имя нового листа.

Если необходимо получить информацию и графики остатков, установите соответствующие флажки в диалоговом окне. Щелкните по кнопке ОК.

Результаты регрессионного анализа представлены на рис.1.10.

 

Рис.1.7.

 

Рис.1.8.

 

 

Рис.1.9.

 

Рис.1.10.

Поясним некоторые обозначения результатов регрессионного анализа:

Множественный R - коэффициент корреляции r_xy;

R-квадрат – коэффициент детерминации;

Стандартная ошибка – СКО объясняемой переменной y;

df - количество степеней свободы;

SS (Регрессия) - объясненная сумма квадратов k_i ².

SS (Остаток) - остаточная сумма квадратов e_i ²;

Коэффициенты (Y-пересечение) – b ₀;

Коэффициенты (минимум(Х)) – b ₁;

Стандартная ошибка(Y-пересечение) – ;

Стандартная ошибка(минимум(Х)) – ;

Нижние (Верхние) – соответствующие границы доверительных интервалов для оценок b ₀ и b ₁.

Как видно функции Линейн и особенно опция Регрессия выводят большинство показателей, которые до этого были рассчитаны с помощью одиночных функций.

 

 

1.3. Контрольные задания

 

Задача 1. В выборке представлены данные по цене (Р) некоторого блага и количеству (Q) данного блага, приобретенному домохозяйством в течение года.

 

Задание.

1. Постройте корреляционное поле и по его виду определите форму зависимости между Р и Q.

2. Оцените по МНК параметры уравнения линейной регрессии.

3. Оцените выборочный коэффициент корреляции и сделайте предварительный вывод о силе линейной взаимосвязи параметров Р и Q.

4. Проверьте качество уравнения регрессии:

- значимость коэффициентов регрессии;

- интервальные оценки коэффициентов регрессии;

- значимость уравнения регрессии в целом.

5. Проинтерпретируйте результаты.

6. Сделайте прогноз количества приобретаемого блага и доверительный интервал для него при значении Р = Р _прогн..

 

Вариант 1.1

месяц

Р

Q

 

Р _прогн= 50; Уровень значимости = 0, 01.

 

Вариант 1.2

месяц

Р

Q

 

Р _прогн= 100; Уровень значимости = 0, 02.

 

Вариант 1.3

месяц

Р

Q

 

Р_прогн= 65; Уровень значимости = 0, 03.

 

Вариант 1.4

месяц

Р

Q

 

Р _прогн= 30; Уровень значимости = 0, 04.

 

Вариант 1.5

месяц

Р

Q

 

Р _прогн= 40; Уровень значимости = 0, 05.

 

Задача 2. Имеются данные об уровне механизации работ Х (%) и производительности труда Y (т/ч) для 14 предприятий.

 

Задание.

1. Постройте корреляционное поле и по его виду определите форму зависимости между Х и Y.

2. Оцените по МНК параметры уравнения линейной регрессии.

3. Оцените выборочный коэффициент корреляции и сделайте предварительный вывод о силе линейной взаимосвязи параметров Х и Y.

4. Проверьте качество уравнения регрессии:

a. значимость коэффициентов регрессии;

b. интервальные оценки коэффициентов регрессии;

c. значимость уравнения регрессии в целом.

5. Проинтерпретируйте результаты.

6. Сделайте прогноз производительности труда и доверительный интервал для нее при значении Х = Х _прогн..

 

Вариант 2.1

хi

yi

 

Х _прогн= 80; Уровень значимости = 0, 02.

 

Вариант 2.2

хi

yi

 

Х _прогн= 80; Уровень значимости = 0, 03.

 

Вариант 2.3

хi

yi

 

Х _прогн= 75; Уровень значимости = 0, 04.

 

Вариант 2.4

хi

yi

 

Х _прогн= 85; Уровень значимости = 0, 05.

 

Вариант 2.5

хi

yi

 

Х _прогн= 90; Уровень значимости = 0, 06.

 

Задача 3. По территориям региона приведены данные в таблице.

 

Задание.

1. Постройте корреляционное поле и по его виду определите форму зависимости между Х и Y.

2. Оцените по МНК параметры уравнения линейной регрессии.

3. Оцените выборочный коэффициент корреляции и сделайте предварительный вывод о силе линейной взаимосвязи параметров Х и Y.

4. Проверьте качество уравнения регрессии:

a. значимость коэффициентов регрессии;

b. интервальные оценки коэффициентов регрессии;

c. значимость уравнения регрессии в целом.

5. Проинтерпретируйте результаты.

6. Сделайте прогноз среднедневной заработной платы и доверительный интервал для нее при значении Х = Х _прогн..

 

 

Вариант 3.1

Номер региона	Среднедушевой прожиточный минимум в день одного трудоспособного, руб., Х	Среднедневная заработная плата, руб., Y

 

Х _прогн= 900; Уровень значимости = 0, 03.

 

Вариант 3.2

Номер региона	Среднедушевой прожиточный минимум в день одного трудоспособного, руб., Х	Среднедневная заработная плата, руб., Y

 

Х _прогн= 1000; Уровень значимости = 0, 04.

 

Вариант 3.3

Номер региона	Среднедушевой прожиточный минимум в день одного трудоспособного, руб., Х	Среднедневная заработная плата, руб., Y

 

Х _прогн= 950; Уровень значимости = 0, 05.

 

Вариант 3.4

Номер региона	Среднедушевой прожиточный минимум в день одного трудоспособного, руб., Х	Среднедневная заработная плата, руб., Y

 

Х_прогн= 980; Уровень значимости = 0, 06.

 

Вариант 3.5

Номер региона	Среднедушевой прожиточный минимум в день одного трудоспособного, руб., Х	Среднедневная заработная плата, руб., Y
Номер региона	Среднедушевой прожиточный минимум в день одного трудоспособного, руб., Х	Среднедневная заработная плата, руб., Y

 

Х _прогн= 820; Уровень значимости = 0, 07.

 

Задача 4. По территориям региона известны данные за 2006 год.

 

Задание.

1. Постройте корреляционное поле и по его виду определите форму зависимости между Х и Y.

2. Оцените по МНК параметры уравнения линейной регрессии.

3. Оцените выборочный коэффициент корреляции и сделайте предварительный вывод о силе линейной взаимосвязи параметров Х и Y.

4. Проверьте качество уравнения регрессии:

a. значимость коэффициентов регрессии;

b. интервальные оценки коэффициентов регрессии;

c. значимость уравнения регрессии в целом.

5. Проинтерпретируйте результаты.

6. Сделайте прогноз доли денежных доходов, направленных на прирост сбережений и доверительный интервал для нее при значении Х = Х _прогн..

 

Вариант 4.1 (Центральный регион)

Номер района	Доля денежных доходов, направленных на прирост сбережений в общей сумме среднедушевого денежного дохода, %, Y	Среднемесячная заработная плата, тыс. руб., Х
	11, 0	10, 0
	9, 0	8, 5
	4, 1	5, 4
	5, 2	6, 0
	6, 5	6, 5
	10, 5	11, 0
	11, 4	12, 3
	8, 1	8, 0
	6, 0	5, 9
Номер района	Доля денежных доходов, направленных на прирост сбережений в общей сумме среднедушевого денежного дохода, %, Y	Среднемесячная заработная плата, тыс. руб., Х
	5, 4	7, 3
	8, 6	9, 0

 

Х _прогн= 13; Уровень значимости = 0, 04.

 

 

Вариант 4.2 (Волго-Вятский регион)

Номер района	Доля денежных доходов, направленных на прирост сбережений в общей сумме среднедушевого денежного дохода, %, Y	Среднемесячная заработная плата, тыс. руб., Х
	4, 0	5, 3
	5, 0	6, 2
	5, 4	7, 4
	5, 1	5, 8
	6, 3	9, 1
	5, 6	8, 3
	6, 5	10, 4
	6, 6	11, 0

 

Х _прогн= 12; Уровень значимости = 0, 05.

 

Вариант 4.3 (Поволжский регион)

Номер района	Доля денежных доходов, направленных на прирост сбережений в общей сумме среднедушевого денежного дохода, %, Y	Среднемесячная заработная плата, тыс. руб., Х
	3, 6	3, 9
	4, 3	5, 1
	4, 2	4, 8
	5, 0	5, 5
	5, 8	6, 7
	6, 0	7, 1
	6, 5	8, 0
	4, 1	4, 5

 

Х _прогн= 8, 5; Уровень значимости = 0, 06.

 

Вариант 4.4 (Северный и Северозападный регионы)

Номер района	Доля денежных доходов, направленных на прирост сбережений в общей сумме среднедушевого денежного дохода, %, Y	Среднемесячная заработная плата, тыс. руб., Х
	5, 1	4, 8
	6, 4	7, 5
	11, 0	10, 4
	12, 1	14, 5
	10, 9	11, 1
	6, 8	8, 3
	6, 0	6, 8
	9, 0	9, 4

 

Х _прогн= 15; Уровень значимости = 0, 07.

 

 

Вариант 4.5 (Дальневосточный регион)

Номер района	Доля денежных доходов, направленных на прирост сбережений в общей сумме среднедушевого денежного дохода, %, Y	Среднемесячная заработная плата, тыс. руб., Х
	4, 0	7, 6
	6, 2	7, 6
	7, 1	10, 5
	11, 5	14, 8
	12, 1	16, 2
	9, 6	10, 7
	7, 0	8, 9
	9, 0	9, 3
	10, 5	12, 0

 

Х _прогн= 18; Уровень значимости = 0, 08.

 

Задача 5. По территориям региона известны данные за 2006 год.

 

Задание.

1. Постройте корреляционное поле и по его виду определите форму зависимости между Х и Y.

2. Оцените по МНК параметры уравнения линейной регрессии.

3. Оцените выборочный коэффициент корреляции и сделайте предварительный вывод о силе линейной взаимосвязи параметров Х и Y.

4. Проверьте качество уравнения регрессии:

a. значимость коэффициентов регрессии;

b. интервальные оценки коэффициентов регрессии;

c. значимость уравнения регрессии в целом.

5. Проинтерпретируйте результаты.

6. Сделайте прогноз размера пенсий при значении прожиточного минимума Х = Х _прогн..

 

 

Вариант 5.1 (Центральный регион)

Номер района	Средний размер назначенных ежемесячных пенсий, тыс. руб., Y	Прожиточный минимум в среднем на одного пенсионера в месяц, тыс. руб., Х
	3, 5	2, 0
	4, 6	2, 2
	5, 5	3, 0
	3, 9	2, 1
	3, 1	1, 8
	4, 2	2, 0
	4, 0	2, 3
	5, 1	2, 5
	3, 7	1, 9
	4, 0	2, 5

 

Х _прогн= 3; Уровень значимости = 0, 01.

 

Вариант 5.2 (Волго-Вятский регион)

Номер района	Средний размер назначенных ежемесячных пенсий, тыс. руб., Y	Прожиточный минимум в среднем на одного пенсионера в месяц, тыс. руб., Х
	3, 2	1, 5
	3, 6	1, 9
	3, 7	2, 0
	4, 0	2, 5
	4, 1	2, 2
	3, 9	2, 1
	4, 5	2, 7
	3, 5	1, 7

 

Х _прогн= 3; Уровень значимости = 0, 03.

 

Вариант 5.3 (Поволжский регион)

Номер района	Средний размер назначенных ежемесячных пенсий, тыс. руб., Y	Прожиточный минимум в среднем на одного пенсионера в месяц, тыс. руб., Х
	3, 5	1, 7
	3, 6	2, 0
	4, 1	2, 3
	5, 1	2, 8
	4, 4	2, 5
	3, 6	1, 9
	4, 0	2, 2
	4, 7	2, 7

 

Х _прогн= 3; Уровень значимости = 0, 05.

 

Вариант 5.4 (Северный и Северозападный регионы)

Номер района	Средний размер назначенных ежемесячных пенсий, тыс. руб., Y	Прожиточный минимум в среднем на одного пенсионера в месяц, тыс. руб., Х
	3, 8	1, 8
	3, 8	1, 9
	4, 1	2, 4
	4, 0	2, 1
	4, 5	2, 7
	4, 3	2, 0
	4, 6	2, 6
	4, 2	2, 5

 

Х _прогн= 3; Уровень значимости = 0, 07.

 

Вариант 5.5 (Дальневосточный регион)

Номер района	Средний размер назначенных ежемесячных пенсий, тыс. руб., Y	Прожиточный минимум в среднем на одного пенсионера в месяц, тыс. руб., Х
	4, 0	2, 0
	4, 1	2, 4
	4, 5	3, 0
	4, 3	2, 8
	5, 0	3, 5
	4, 2	1, 9
	4, 2	3, 1
	5, 2	3, 7
	4, 7	3, 3

 

Х _прогн= 4; Уровень значимости = 0, 09.

Задача 6. По территориям региона известны данные за 2006 год.

Задание.

1. Постройте корреляционное поле и по его виду определите форму зависимости между Х и Y.

2. Оцените по МНК параметры уравнения линейной регрессии.

3. Оцените выборочный коэффициент корреляции и сделайте предварительный вывод о силе линейной взаимосвязи параметров Х и Y.

4. Проверьте качество уравнения регрессии:

a. значимость коэффициентов регрессии;

b. интервальные оценки коэффициентов регрессии;

c. значимость уравнения регрессии в целом.

5. Проинтерпретируйте результаты.

6. Сделайте прогноз потребительских расходов при средней заработной плате и выплатах социального характера Х = Х _прогн..

 

Вариант 6.1 (Центральный регион)

Номер района	Потребительские расходы на душу населения, тыс. руб., Y	Средняя заработная плата и выплаты социального характера, тыс. руб., Х
	7, 0	11, 0
	6, 1	9, 5
	4, 9	6, 4
	5, 1	6, 9
	4, 8	7, 4
	7, 1	12, 0
	7, 5	12, 9
	6, 0	9, 0
	4, 8	7, 0
	5, 3	8, 2
	6, 7	10, 0

 

Х _прогн= 13, 5; Уровень значимости = 0, 01.

 

Вариант 6.2 (Волго-Вятский регион)

Номер района	Потребительские расходы на душу населения, тыс. руб., Y	Средняя заработная плата и выплаты социального характера, тыс. руб., Х
	4, 3	6, 4
	5, 0	7, 5
	5, 4	9, 0
	4, 6	7, 0
	5, 2	10, 9
	5, 1	9, 3
	7, 0	11, 2
	7, 5	12, 4

 

Х _прогн= 13; Уровень значимости = 0, 02.

Вариант 6.3 (Поволжский регион)

Номер района	Потребительские расходы на душу населения, тыс. руб., Y	Средняя заработная плата и выплаты социального характера, тыс. руб., Х
	3, 2	4, 9
	4, 0	6, 2
	4, 0	6, 0
	4, 4	6, ⇐ Предыдущая12345678910Следующая ⇒ Дата добавления: 2014-11-10; просмотров: 878. Нарушение авторских прав; Мы поможем в написании вашей работы! Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где... Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса... Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар... Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения... Билиодигестивные анастомозы Показания для наложения билиодигестивных анастомозов: 1. нарушения проходимости терминального отдела холедоха при доброкачественной патологии (стенозы и стриктуры холедоха) 2. опухоли большого дуоденального сосочка... Сосудистый шов (ручной Карреля, механический шов). Операции при ранениях крупных сосудов 1912 г., Каррель – впервые предложил методику сосудистого шва. Сосудистый шов применяется для восстановления магистрального кровотока при лечении... Трамадол (Маброн, Плазадол, Трамал, Трамалин) Групповая принадлежность · Наркотический анальгетик со смешанным механизмом действия, агонист опиоидных рецепторов... ТЕРМОДИНАМИКА БИОЛОГИЧЕСКИХ СИСТЕМ. 1. Особенности термодинамического метода изучения биологических систем. Основные понятия термодинамики. Термодинамикой называется раздел физики... Травматическая окклюзия и ее клинические признаки При пародонтите и парадонтозе резистентность тканей пародонта падает... Подкожное введение сывороток по методу Безредки. С целью предупреждения развития анафилактического шока и других аллергических реак­ций при введении иммунных сывороток используют метод Безредки для определения реакции больного на введение сыворотки...

Studopedia.info - Студопедия - 2014-2025 год . (0.013 сек.) русская версия | украинская версия