Элементарные задачи на принадлежность
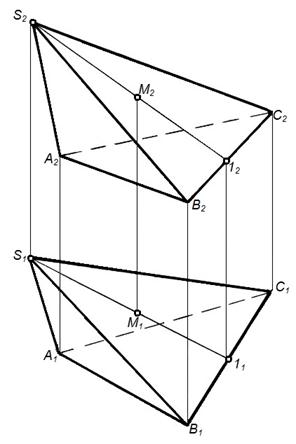
1. Построить линию, принадлежащую многогранной поверхности. На рисунке 39 построены прямолинейные отрезки [1-2] и [S-3], принадлежащие поверхности пирамиды. 2. Построить вторую проекцию линии, принадлежащую многогранной поверхности. На рисунке 40 – отрезок [1-2], принадлежащий поверхности призмы.
Рисунок 39 – Линия на поверхности пирамиды
Рисунок 40 – Линия на поверхности призмы
Рисунок 41 – Условие задачи на построение линии
На рисунке 41 дано исходное условие задачи – фронтальная проекция l2 линии l, принадлежащей поверхности призмы
Рисунок 42 – Решение задачи на построение прямой На рисунке 42 задача решена.
3 Построить точку, принадлежащую многогранной поверхности.
Рисунок 43 – Точка на поверхности пирамиды
На рисунке 43 построена точка М, принадлежащая поверхности пирамиды, т.к. она принадлежит линии S1(S111; S212), принадлежащей данной поверхности.
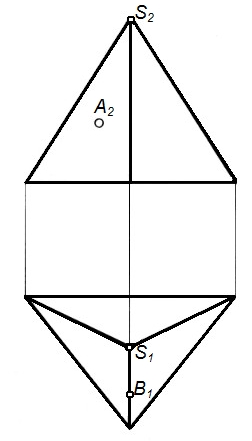
Задача построить вторую проекцию точки, принадлежащей многогранной поверхности, если одна, ее проекция задана. На рисунке 44 даны исходные условия, т.е. заданы проекции точек А2 и B1. Достроить их недостающие проекции.
Рисунок 44 – Условие задачи на нахождение точек пирамиды
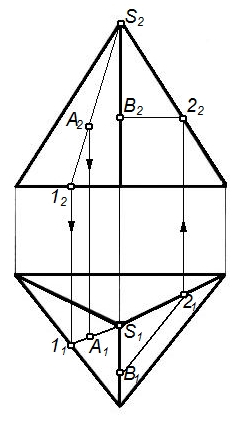
Рисунок 45 – Построение недостающих проекций точек пирамиды На рисунке 45 построение вторых проекций точек A и B, принадлежащих поверхности пирамиды.
|