Однополостный гиперболоид вращения

На рисунке 51 поверхность имеет две образующие линии l (BC) и l' (B'C') наклоненные в разные стороны и пересекающиеся в толчке (А), принадлежащей наименьшей параллели.

Отрезок ОА является кратчайшим расстоянием между образующей и осью. Таким образом, на поверхности однополостного гиперболоида располагаются два семейства прямолинейных образующих. Все образующие одного семейства – скрещивающиеся прямые. Каждая образующая одного семейства пересекает все образующие другого. Через каждую точку поверхности проходят две образующие разных семейств. Меридианом поверхности является гипербола.

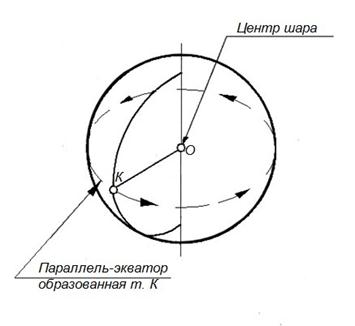
Рисунок 51 – Поверхность вращения – однополостный гиперболоид

Поверхности, образуемые при вращении окружности

Сфера

Тело, полученное от вращения полукруга вокруг диаметра, называется шаром, а поверхность, образуемая при этом окружностью, называется сферической (рисунок 52).

Можно также сказать, что эта поверхность есть геометрическое место точек, одинаково удаленных от одной и той же точки, называемой центром. Отрезок, соединяющий центр с какой-нибудь точкой поверхности, называется радиусом, а отрезок, соединяющий две точки поверхности и проходящий через центр, называется диаметром сферы.

На рисунке 52 ось вращения сферической поверхности совпадает с вертикальным диаметром.

Всякая проекция сферической поверхности является окружностью, очерками проекций на плоскость П1 является проекция экватора, на плоскость П2 и П3 являются проекции меридианов.

Рисунок 52 – Поверхность вращения - сфера

 

На рисунке 53 отмечены проекции оси i, экватора b, фронтального меридиана а и профильного l.

Задача 1. Построить проекции точек А и В, принадлежащие сфере рисунок 53.

Недостающие проекции точек, определяются с помощью параллелей, которым эти точки принадлежат.

Видимость точек А и В определена в зависимости от того, на какой части сферы они лежат (на видимой части – видимы, на невидимой – невидимы).

 

 

Рисунок 53 – Определение видимости сферы

 

Задача 2. Построить недостающие проекции видимых линий, принадлежащих поверхности сферы.

На рисунке 54а показано построение А1В1С1 и А3В3С3 по заданной А2В2С2; L1K1 и L3K3 по заданной L2K2; M2N2 и M1N1 по заданной M3K3.

На рисунке 54б показано построение А3В3С3D3E3K3 по заданной А2В2С2D2E2K2.

 

а)

б)

Рисунок 54 – Построение линий на поверхности сферы