Построение линии пересечения двух поверхностей
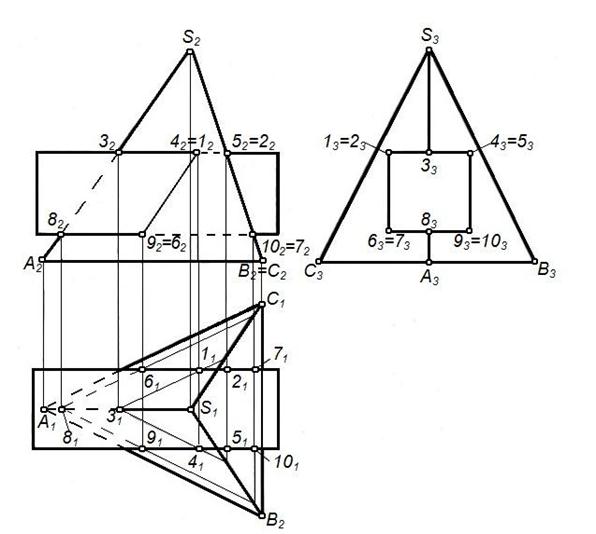
Для решения задач на построение линии пересечения двух поверхностей общего положения в качестве вспомогательной поверхности (посредник), следует выбирать такие, которые пересекали бы заданные по наиболее простым для построения линиям – прямым или окружностям. В качестве вспомогательных поверхностей (посредников) наиболее часто используются секущие плоскости и сферические поверхности. Прежде чем решить вопрос, какие вспомогательные поверхности следует выбрать необходимо, выяснить, не занимает ли одна из пересекающихся поверхностей проецирующее положение, т.к. в данном случае решение поставленной задачи значительно упрощается. Это происходит из-за того, что одна из проекций линии пересечения будет совпадать с главной проекцией проецирующей поверхности. Поэтому решение сводится к определению недостающей проекции линии, принадлежащей заданным поверхностям из условия принадлежности. Пример решение задач: Задача. Построить линию пересечения пирамиды и призмы (рисунок 69) 1. Заданы многогранники. Все ребра призмы пересекают грани пирамиды. Имеем случай проницания. Призма занимает профильно-проецирующее положение. 2. Так как призма перпендикулярна П3, то профильная проекция линии пересечения заданных многогранников совпадает с профильной проекцией призмы. 3. Линия пересечения распалась на две замкнутые ломаные линии: пространственную 1-6-8-9-4-3-1 и плоскую 2-5-10-7-2. Фронтальная и горизонтальная проекция линии пересечения построена из условия принадлежности пирамиды. 4. Отрезки прямых соединены с учетом видимости. Видимыми считаются те участки ломаной, которые являются линией пересечения двух видимых граней многогранника и наоборот.
Рисунок 69 – Пересечение пирамиды и призмы
Задача. Построить проекции линии пересечения конуса и треугольной призмы (рисунок 70). 1. Линия состоит из совокупности дуги окружности, части гиперболы и части эллипса. 2. Так как призма фронтально-проецирующая, то фронтальная проекция линии пересечения совпадает с фронтальной проекцией призмы. 3. Горизонтальная и профильная проекции линии пересечения построены из условия принадлежности конусу.
Рисунок 70 – Пересечение конуса и призмы
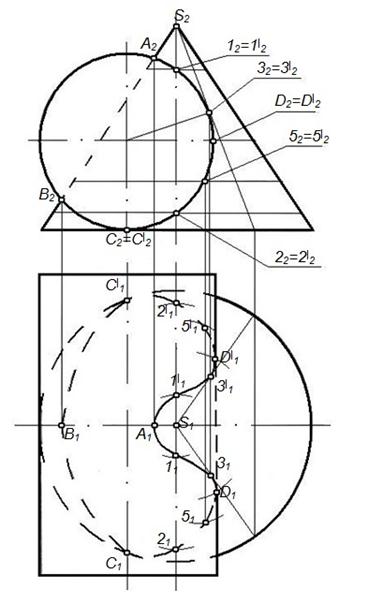
Задача. Построить линию пересечения конуса и цилиндра (рисунок 71) 1. Заданы кривые поверхности. Случай врезки. Цилиндр занимает фронтально-проецирующее положение 2. Линия пересечения – пространственная замкнутая кривая 3. Так как цилиндр занимает фронтально-проецирующее положение, то фронтальная проекция линии пересечения заданных поверхностей совпадает с фронтальной проекцией цилиндра, а горизонтальная проекция строится по принадлежности конусу.
Рисунок 71 – Пересечение конуса и цилиндра
4. Опорные точки: А, С, С¢ – экстремальные. А – высшая точка, С, С¢ - низшие, D, D¢ – очерковые (точки смены видимости на П1). Точки 1, 1¢ и 2, 2¢ – очерковые относительно П3. Точки 3, 3¢ – точки касания образующих конуса и цилиндра. Остальные точки – промежуточные. 5. Соединив полученные точки плавной кривой с учетом видимости, получим горизонтальную проекцию линии перемещения заданных поверхностей.
|