Позиционные задачи на пересечение прямой линии с поверхностью

 

В зависимости от вида и взаимного расположения линии и поверхности точек пересечения может быть одна или несколько. Например, прямая линия с плоскостью пересекается в одной точке, а с кривыми поверхностями в n точках. В основу их построения положен способ вспомогательных секущих плоскостей, сущность которого состоит в том, что каждая из искомых точек рассматривается как результат пересечения двух линий, принадлежащих вспомогательной плоскости. Одна из них является заданной прямой линией, а вторая – линией пересечения вспомогательной плоскости и заданной поверхности.

Рисунок 79 – Пересечение линии и поверхности

Построение точек пересечения линии l и поверхности Æ (независимо от их вида) осуществляется по общей схеме (рисунок 80).

1. Через l проводим вспомогательную плоскость S.

2. Определяем линию m пересечения вспомогательной S и заданной Æ поверхностей.

3. Отмечаем точку K пересечения l и m, которая и является искомой.

Рисунок 80 – Пересечение прямой с плоскостью

 

Для простоты и точности построения на комплексном чертеже вспомогательную плоскость следует выбирать так, чтобы проекции линии ее пересечения с заданной поверхностью были графически простыми линиями, т.е. прямимы линиями или окружностями.

Ниже рассмотрим примеры решения типовых задач на определение точек пересечение прямой линии и поверхности. Алгоритмы их решения составлены в соответствии с общей схемой решения.

Задача 1. Определение точки пересечения прямой общего положения с плоскостью общего положения.

При определении точки K пересечения прямой l с плоскостью Æ (АВС) (рисунок 81) в качестве вспомогательной плоскости выбираем проецирующую плоскость S и составим алгоритм решения:

1. Заключаем прямую l в горизонтально-проецирующую плоскость S;

2. Определяем линию пересечения 1-2 плоскостей Æ и S;

3. Отмечаем точку K пересечения линии 1-2 и l, которая и является искомой.

Рисунок 81 – Графическое изображение пересечение прямой и плоскости общего положения

Видимость прямой l и заданной поверхности Æ определяется с помощью конкурирующих точек. Видимость на П1 определена с помощью горизонтально-конкурирующих точек 1, 3, а на П2 – с помощью фронтально-конкурирующих 4, 5. Плоскость Æ (АВС) считается непрозрачной.

Задача 2. Определение точек пересечения прямой линии с поверхностью многогранника.

Решение этой задачи сводится к определению точек пересечения прямой с гранями многогранника и выполняется по предыдущему алгоритму.

Определение точек M и N пересечения прямой l с поверхностью призмы показано на рисунке 82.

 

Рисунок 82 – Пересечение прямой и призмы

 

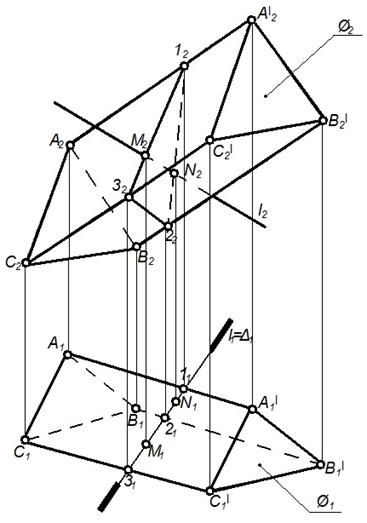
Алгоритм:

1. Прямую l заключаем в плоскость D, D^П1 (может быть выбрана D^П2);

2. Определяем линию пересечения (1-2-3) плоскости D с поверхность Æ;

3. M= (1-2-3)∩ l;

4. N=(1-2-3)∩ l;

Поверхность многогранника считается непрозрачной. Видимость проекций прямой l определяется по видимости граней многогранника.

Рассмотренный алгоритм применим для определения точек пересечения прямой с любым многогранником.

 

 

Рисунок 83 – Графическое изображение пересечения прямой и призмы

Задача 3. Определение точек пересечения прямой линии с поверхностью конуса.

В задаче (рис.93) требуется определить точки M и N пересечения горизонтали h с поверхностью конуса вращения Æ.

Рисунок 84 – Графическое изображение пересечения прямой и конуса

 

В данном случае целесообразно через прямую h провести горизонтальную плоскость уровня Г, т.к. она пересечет поверхность конуса по параллели m, которая проецируется на П1 без искажения.

Алгоритм:

1. Заключаем горизонталь h в плоскость Г (ГÌ h; Г‖ П1);

2. При пересечении плоскости Г с конусом получается окружность m (m=φ ∩ Г).

3. M=m∩ h; N=m∩ h.

Задача 4. Определение точек пересечения прямой линии и сферы.

В задаче (рисунок 85) требуется определить точки M и N пересечения сферы Ө с фронталью f. В качестве вспомогательной плоскости целесообразно применить фронтальную плоскость уровня D, так как окружность m сечения сферы Ө этой плоскостью проецируется на П2 без искажения.

 

Рисунок 85 - Графическое изображение пересечения прямой и сферы

 

 

Алгоритм:

1. Заключаем фронталь f в плоскость D (DÌ f; D‖ П2);

2. При пересечении плоскости D со сферой получается окружность m (m= Ө ∩ D).

3. M=m∩ f; N=m∩ f.