ЗАДАЧА 9. Условие задачи: Построить точки пересечения прямой (A,B) с поверхностью наклонного цилиндра с круговыми основаниями

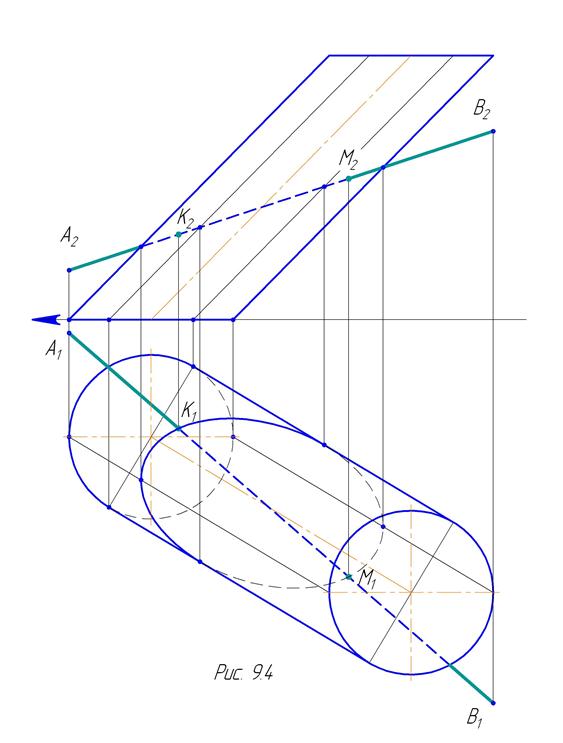
Условие задачи: Построить точки пересечения прямой (A, B) с поверхностью наклонного цилиндра с круговыми основаниями, одно из которых принадлежит горизонтальной плоскости проекций P₁. Определить видимость прямой (A, B) относительно поверхности цилиндра (приложение 7).

Общие указания: задачу необходимо выполнить на двухкартинном чертеже простым карандашом на половине формата А3 в масштабе 1: 1 совместно с задачей 10 (см. ниже), которую располагают на другой половине формата А3.

Пример решения: на рисунке 9.1 построены проекции прямой и цилиндра. Очерковые цилиндра на P₁ построены с помощью вспомогательных отрезков, проходящих через проекции центров окружностей основания и перпендикулярных оси цилиндра. Половина окружности нижнего основания не видна на P₁.

Задача решается по следующему алгоритму:

— через прямую (A, B)проводят вспомогательную проецирующую плоскость S. На рис. 9.2 плоскость S — фронтально проецирующая (S₂ º ( A ₂, B ₂));

— плоскость S пересекает цилиндр по эллипсу, проекция которого на P₂ отрезок [ 1₂; 4₂ ], совпадающий со следом вспомогательной плоскости S₂: точка 1 принадлежит очерковой образующей, проходящей через точку 5 основания, точка 4 — очерковой образующей, проходящей через точку 8 основания (рис. 9.3). Промежуточные точки 2 и 3 тоже являются характерными. Они принадлежат очерковым образующим цилиндра на P₁, проходящим через точки 6 и 7 основания. Горизонтальная проекция эллипса построена с учетом видимости: от точки 1 до точек 2 и 3 видна, к точке 4 — нет. На рис. 9.3 для эллипса построены только характерные точки, для более точного построения необходимо взять промежуточные: между точками 1 и 2, 2 и 3, 3 и 4, и построить их проекции на P₁ с помощью образующих цилиндра;

— точки пересечения K, M прямой (A, B) с эллипсом (рис. 9.4) есть искомые точки пересечения с цилиндром. Точка K принадлежит видимой на P₁ части цилиндра, точка M — не видимой на P₁ части цилиндра.

Если точка пересечения видна на данной плоскости проекций, то прямая тоже видна и наоборот. Поверхность цилиндра непрозрачна, поэтому между точками пересечения прямая не видна. Точка M на P₂ видна (принадлежит видимой на P₂ образующей), поэтому видна и проекция прямой (A, B) правее точки M _{2 .}. Точка K на P₂ не видна, поэтому не видна и проекция прямой (A, B) левее точки K ₂, пока прямая не вышла из за очерка цилиндра.

Решение задачи 9 выше предложенным способом является не точным, но общим для всех остальных поверхностей, когда необходимо найти точки пересечения прямой с данной поверхностью. Если в пересечении участвует цилиндр, то для точного нахождения точек пересечения вспомогательную секущую плоскость проводят не проецирующую, а параллельную образующим цилиндра. Тогда в пересечении с цилиндром получают прямолинейные образующие, а не кривые линии. Подробно смотри в любой учебной литературе по начертательной геометрии [1], [3].