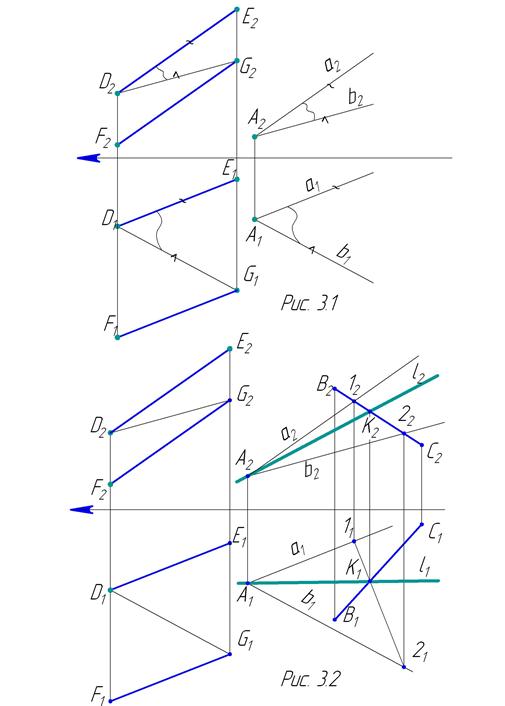
ЗАДАЧА 4. Условие задачи: построить прямую пересечения плоскостей S(DE || FG)и Q(ABC) (приложение
Условие задачи: построить прямую пересечения плоскостей S (DE || FG)и Q (ABC) (приложение. 2). Общие указания: задачу необходимо выполнить на двух картинном чертеже простым карандашом на половине формата А3 в масштабе 1: 1 совместно с задачей 3 (см. выше), которую располагают на другой половине формата А3.
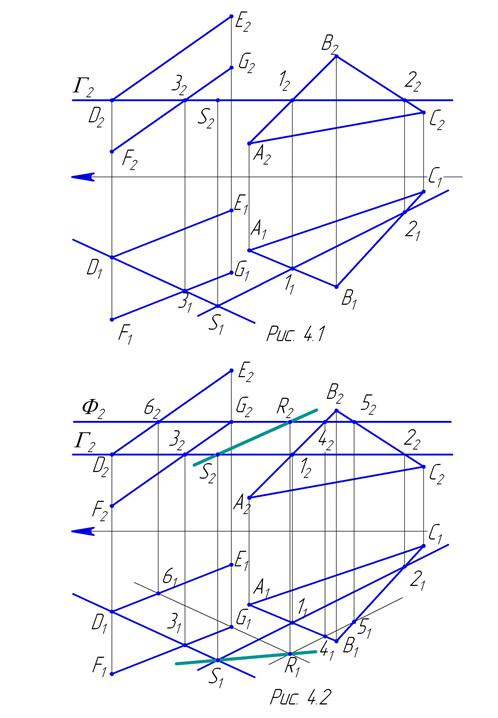
Пример решения: на рисунке 4.1 по трем координатам построены по две проекции каждой из заданных точек: A, B, C, D, E, F, G. Задача решается способом вспомогательных секущих плоскостей. Вводят две плоскости частного положения, пересекающие заданные плоскости. С их помощью находят две точки, общие для двух заданных плоскостей. Соединяют точки прямой, которая и есть искомая. На рис. 4.1 вспомогательная плоскость G — горизонтальная плоскость уровня — пересекает плоскость S (DE || FG)по прямой (D; 3), плоскость Q (ABC)по прямой (1; 2), в пересечении прямых (D; 3) и (1; 2) получают общую точку S. На рис. 4.2. введена вторая вспомогательная плоскость F, параллельная плоскости G, которая пересекает плоскость S (DE || FG) по прямой (6; G), плоскость Q (ABC)по прямой (4; 5), в пересечении прямых (6; G) и (4; 5) получают общую точку R. Прямая (SR) – искомая. Для того чтобы ответ получился в пределах отведённого поля чертежа, не всегда можно применить в качестве вспомогательных горизонтальные плоскости уровня. Это могут быть и фронтальные плоскости уровня, и проецирующие. На рисунках 4.3 и 4.4 даны варианты вспомогательных секущих проецирующих плоскостей W и D, проведённых через прямые, задающие плоскости: горизонтально проецирующая W через сторону треугольника AB и горизонтально проецирующая D через прямую FG. С помощью плоскости W найдена общая точка T, с помощью плоскости D найдена общая точка P.
|