ЗАДАЧА 8. Условие задачи: Построить проекции линии пересечения сферы радиусом 40 мм и центром O(55;60;75) с проецирующей плоскостью Σ
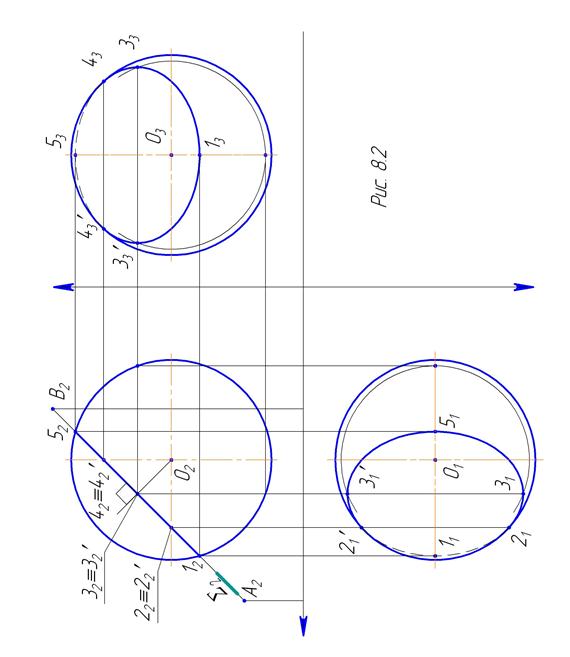
Условие задачи: Построить проекции линии пересечения сферы радиусом 40 мм и центром O (55; 60; 75) с проецирующей плоскостью Σ;, след которой задается точками A и B (приложение 6). Общие указания: задачу необходимо выполнить на трёхкартинном чертеже простым карандашом на формате А3 в масштабе 1: 1. Пример решения: на рисунке 8.1 построены три проекции сферы и горизонтальный след Σ 1 горизонтально проецирующей плоскости Σ (для вариантов, когда точки A, B заданы координатами x и y, по координате z — прочерк). Плоскость S (как любая другая плоскость)пересекает сферу по окружности, проекция которой на P1 отрезок [ 11; 51 ], совпадающий со следом плоскости S1, проекции на P2 и P3 — эллипсы с осями [ 1; 5 ] и [ 3; 3¢ ]. Точки 3 1 º 31¢ — середина отрезка [ 11; 51 ], недостающие проекции которых построены с помощью окружностей на сфере, параллельных соответствующим плоскостям проекций (параллелей). Промежуточные точки 2 и 2¢ принадлежат границе видимости сферы на P2, точки 4 и 4¢ — границе видимости сферы на P3. Фронтальная проекция линии пересечения построена с учетом видимости: от точки 1 до точек 2 и 2¢ линия видна, к точке 5 не видна. Линия пересечения на P3 видна от точки 1 до точек 4 и 4¢, не видна к точке 5. На рис. 8.1 для эллипсов — проекций окружности — построены только характерные точки, для более точного построения необходимо взять промежуточные: между точками 1 и 2, 2 и 3, 3 и 4, 4 и 5 и построить их проекции на P2 и P3 с помощью параллелей сферы. На рисунке 8.2 построены три проекции сферы и фронтальный след Σ 2 фронтально проецирующей плоскости Σ (для вариантов, когда точки A, B заданы координатами x и z, по координате y — прочерк). На рисунке 8.3 построены три проекции сферы и профильный след Σ 3 профильно проецирующей плоскости Σ (для вариантов, когда точки A, B заданы координатами y и z, по координате x — прочерк).
|