ЗАДАЧА 6. Условие задачи: Построить линию пересечения горизонтально проецирующей призмы KMNK¢M¢N¢ с пирамидой SABCD
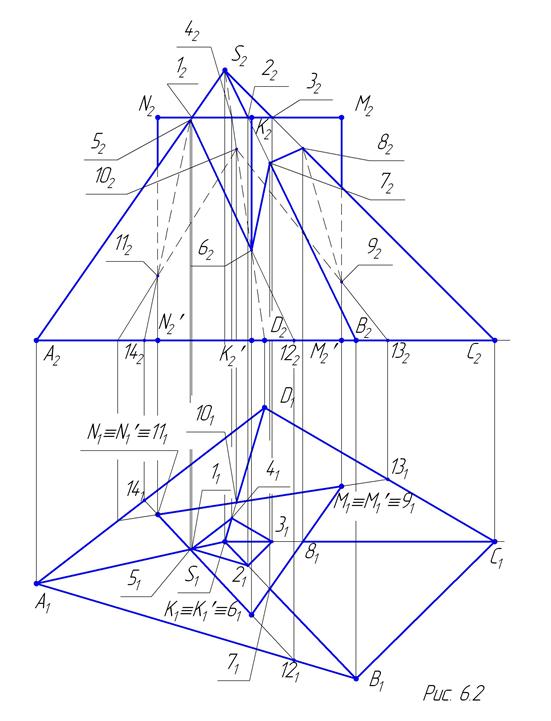
Условие задачи: Построить линию пересечения горизонтально проецирующей призмы KMNK ¢ M ¢ N ¢ с пирамидой SABCD. Определить видимость линии пересечения и ребер многогранников (приложение 4). Общие указания: задачу необходимо выполнить на двухкартинном чертеже простым карандашом на половине формата А3 в масштабе 1: 1 совместно с задачей 5 (см. выше), которую располагают на другой половине формата А3. Пример решения: на рисунке 6.1 по трем координатам построены по две проекции каждой из заданных точек: S, A, B, C, D, K, M, N, K ¢;, M ¢;, N ¢;. На рис. 6.2 линия пересечения пирамиды с горизонтально проецирующей прямой призмой распадается на два замкнутых многоугольника: плоский [ 1; 2; 3; 4 ] — пересечение верхней грани призмы с пирамидой и пространственный [ 5; 6; 7; 8; 9; 10; 11 ] – пересечение боковых граней призмы (отсеков горизонтально проецирующих плоскостей) с боковыми гранями пирамиды. Фронтальная проекция многоугольника [ 12223242 ] совпадает с фронтальной проекцией верхней грани призмы [ K 2 M 2 N 2], отсека горизонтальной плоскости уровня, но в пределах очерка пирамиды. Горизонтальную проекцию четырёхугольника строят из условия принадлежности точки 1 ребру SA пирамиды, точки 2 ребру SB, точки 3 ребру SC, точки 4 ребру SD. Получают четырехугольник [ 11213141 ], подобный четырёхугольнику основания пирамиды A 1 B 1 C 1 D 1. Горизонтальная проекция многоугольника [ 5161718191101111 ] совпадает с горизонтальной проекцией призмы. Фронтальную проекцию многоугольника строят из условия принадлежности точки 5 ребру SA, точки 7 ребру SB, точки 8 ребру SC, точки 10 ребру SD. Точку 6 строят из условия принадлежности прямой (5; 12), принадлежащей грани пирамиды ASB, точку 9 из условия принадлежности прямой (10; 13), принадлежащей грани пирамиды CSD, точку 11 из условия принадлежности прямой (5; 14), принадлежащей грани пирамиды ASD. Видимость сторон многоугольника сечения определяется из условия видимости граней многогранников. Если сторона принадлежит видимым граням и пирамиды, и призмы, то она видима; если не видна хотя бы одна из граней, то отрезок линии пересечения невидим. Например, отрезок [ 5; 6 ] принадлежит видимым на P2 граням ASB пирамиды и KNN ¢ K ¢ призмы, поэтому на P2 он видим; отрезок [ 8; 9 ] принадлежит видимой на P2 грани KMM ¢ K ¢ призмы и не видимой на P2 грани CSD пирамиды, поэтому на P2 он не видим.
Считают, что многогранники существуют только до линии пересечения, поэтому участки ребер одного многогранника, расположенные внутри другого многогранника, изображают тонкой сплошной линией. На горизонтальной плоскости это отрезки [ 1151 ], [ 2171 ], [ 3181 ], [ 41101 ]; на фронтальной плоскости - отрезки [ 1252 ], [ 2272 ], [ 3282 ], [ 42102 ], [ 62 K 2¢ ], [ 92 M 2¢ ], [ 112 N 2¢ ].
|