Задача 3. Определить ток в цепи конденсатора (рис
Определить ток в цепи конденсатора (рис. 3.1), если Е=200 В, С=2 мФ, R1=R2=10 Ом, UС(0_)=100 B. Построить графики зависимости i=f(t), UC(t).
Рис. 4.5 Прежде всего, необходимо осознать условие задачи. Понятно, что при разомкнутом ключе в установившемся режиме напряжения на конденсаторе быть не может, ибо он непрерывно разряжается (до нуля) через сопротивления R1 и R2. Условие UС(0_)=100 B означает, что в процессе разрядки в предыдущем переходном процессе при достижении напряжения на конденсаторе 100 В происходит замыкание ключа и начинается новый переходной процесс. В связи с тем, что ветви с R1 и R2, С соединены параллельно, электромагнитные процессы в каждой из них происходят независимо друг от друга под влиянием источника Е. Понятно, что в этом переходном процессе мы имеем дело с двумя в определенном смысле не зависящими друг от друга цепями: Е- R1 и Е-С-R2 (общая ветвь пока не рассматривается). В ветви с R1 ток и напряжение изменяются скачком от первоначальных значений до Переходной процесс здесь отсутствует в связи с отсутствием накопителей энергии. Расчет переходного процесса во второй цепи состоит в следующем. 1 Уравнение электрического равновесия для этой цепи 2 Приведение этого уравнения к одному с одним неизвестным производится на основании того, что
Таким образом, уравнение п. 1 может быть приведено - либо к - либо к Если нас интересует процесс перезарядки конденсатора, решение задачи целесообразно свести к решению первого уравнения. Характеристическое уравнение в этом случае pR2C+1=0. Легко видеть, что это уравнение могло быть получено по входному сопротивлению цепи в комплексной форме после коммутации Отсюда При этом полезно обратить внимание на то, что в случае, если мы будем решать второе дифференциальное уравнение (для тока), характеристическое уравнение цепи будет точно таким же, а именно Корень этого уравнения 3 Решение для свободной составляющей напряжения на конденсаторе имеет вид 4 Находим принужденную составляющую напряжения на конденсаторе
5 Составляем общее выражение (функцию) для переходного напряжения как сумму свободной и принужденной составляющих
6 Находим значение напряжения на конденсаторе в момент t=0 на основании второго закона коммутации uC(0)=uC(0-)=100B 7 Определяем постоянную интегрирования А из уравнения п.5 uC(0)=200+А=100 А=-100В 8 Записываем окончательное уравнение для переходного напряжения конденсатора uC=200-100е-50t 9 Ток I в цепи конденсатора найдем как
10 По полученным уравнениям для тока i и напряжения uC строим графики i=f(t) и uC(t).
Рис. 4.6 Постоянная времени и по току, и по напряжению τ =1/р=1/50=0, 02 с. Понятно, что ток в общей ветви и источнике есть результат наложения (сложения) токов в обеих ветвях, то есть i(t)=i1(t)+i2(t)=20+0, 01e-50t.
|


 и
и 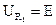 .
. .
.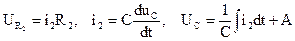 .
.
 , которое после дифференцирования приобретает вид
, которое после дифференцирования приобретает вид  , поскольку
, поскольку  .
. при замене jω на р и приравнивании z(p) к нулю, то есть
при замене jω на р и приравнивании z(p) к нулю, то есть  → R1(R2pC+1)=0→ R2pC=0.
→ R1(R2pC+1)=0→ R2pC=0. .
. .
. .
.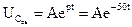 .
. .
. .
.




