Теоретические основы расчета
Теоретической основой операторного метода являются основные положения операционного исчисления, в частности, основные свойства функций-оригиналов f(t) и соответствующих им функций-изображений F(p). Определение функции-изображения по заданной исходной функции может производиться с помощью интеграла Лапласа
либо, что в основном и делается, - по соответствующим готовым таблицам оригиналов и изображений. К наиболее часто используемым в электротехнике операторным изображениям функций относятся: - изображение неизменной во времени функции f(t)=A=const: - изображение синусоидальной функции времени - изображение экспоненциальной функции времени К основным математическим действиям над функциями-оригиналами и соответствующим им действиям над их операторными изображениями относятся следующие: 1) Сложению и вычитанию функций-оригиналов (как и в символическом методе) соответствует сложение и вычитание операторных изображений этих функций, то есть если fk(t)→ Fk(p), то Под символом Это приводит к тому, что первый и второй законы Кирхгофа в операторной форме, как и в символической, приобретают вид:
где Ik(p)← ik(t), Ek(p) ← ek(t) и Uk(p)← Uk(t) есть операторные изображения реальных токов, ЭДС и напряжений в каждой k-ой ветви и на каждом k-том элементе схемы. Это означает, что формулировка первого и второго законов Кирхгофа для операторных изображений токов и напряжений полностью совпадает с их формулировкой для токов и напряжений в цепях постоянного тока. 2) Умножению или делению функции-оригинала на постоянную величину соответствует умножение или деление на эту постоянную операторного изображения оригинала, то есть, если fk(t)→ Fk(p), то k·fk(t)→ k·Fk(p). Это означает, например, что закон Ома для участка цепи с активным сопротивлением R и проводимостью G, то есть
то есть полностью соответствует формулировке закона Ома для участков цепей постоянного тока. 3) Дифференцированию функции-оригинала В этой связи соотношение между током в катушке индуктивности L и напряжением на ее зажимах, формируемое законом электромагнитной индукции (с учетом свойства пункта 2):
При f(0)=0 4) Интегрированию функции-оригинала в операторной форме соответствует (с учетом пункта 1):
Здесь f(0) – значение функции f(t) при t=0, то есть постоянная интегрирования. Операторное изображение этой неизменной во времени функции есть В задачах электротехники это приводит к тому, что операторное изображение напряжения на емкости, определяемое известным соотношением
При UC(0)=0 Все это означает, что в отличие от символического метода расчета цепей в установившемся режиме, когда все функции синусоидальны и постоянные интегрирования всегда равны нулю, в операторной форме ненулевые начальные условия должны быть учтены либо как дополнительно вносимые падения напряжения в правой части второго закона Кирхгофа -LiL(0) и Например, любая ветвь сколь угодно сложной электрической цепи (обобщенный приемник электрической энергии), представленная на рисунке 3.1 и описываемая уравнением (3.1), при переводе ее в область операторных изображений приобретает вид рисунка 3.2 и описывается уравнением (3.2).
Рис. 3.1
Рис. 3.2
Понятно, что уравнение (3.2) есть операторная форма реального уравнения (3.1), где U(p)→ U(t), I(p)→ i(t), UR(t)→ i(t)·R, При этом операторное уравнение составлено на основании того, что сложению функций-оригиналов соответствует сложение функций-изображений. Однако, это операторное уравнение может быть составлено без составления уравнения (3.2) на основании операторной версии второго закона Кирхгофа для цепи рисунка 3.2, если эта схема будет предварительно составлена. Например, для случая ненулевых начальных условий в цепи рисунка 2.1, когда i1≠ 0 и UC3≠ 0, операторная версия этой цепи будет иметь вид
Рис. 3.3
При нулевых начальных условиях Li(0)=0 и Из уравнения (3.2) следует, что для обобщенного приемника электрической энергии (последовательного соединения R, L, C)
Это выражение часто называется законом Ома в операторной форме. При нулевых начальных условиях это выражение полностью совпадает с законом Ома в символической форме (jω → p). Уравнения законов Кирхгофа для цепи рисунка 3.1 в ее операторной версии рисунка 3.3. имеют следующий вид: I1(p)-I2(p)-I3(p)=0; E(p)+Li(0)=I1(p)·R1+I1(p)·pL1+I2(p)·R2;
Операторная форма уравнений по методу контурных токов: E(p)+Li(0)=II(p)[R1+pL1+R2]-III(p)R2
Как уже было отмечено, в операторной версии электрическая цепь может быть рассчитана любым из методов расчета электрических цепей постоянного тока. Рассчитываемая цепь, например, может быть рассчитана методом двух узлов:
Здесь
|

 ,
, ;
; ;
;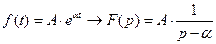 .
. .
. здесь следует понимать алгебраические сложение (с учетом знака каждой функции).
здесь следует понимать алгебраические сложение (с учетом знака каждой функции). ,
, в операторной форме будет иметь вид:
в операторной форме будет иметь вид:
 в операторной форме соответствует
в операторной форме соответствует 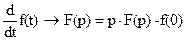 , где f(0) – значение f(t) при t=0. В случае, если f(t)=0,
, где f(0) – значение f(t) при t=0. В случае, если f(t)=0,  . Это полностью совпадает с символическим методом при р→ јω.
. Это полностью совпадает с символическим методом при р→ јω.
 , что в полной мере соответствует комплексному изображению падения напряжения на идеальной индуктивности при р→ јω.
, что в полной мере соответствует комплексному изображению падения напряжения на идеальной индуктивности при р→ јω. .
. . При f(0)=0
. При f(0)=0  , то есть полностью (при р→ јω) совпадает с символическим методом.
, то есть полностью (при р→ јω) совпадает с символическим методом.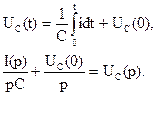
 , как в символическом методе при р→ јω.
, как в символическом методе при р→ јω. , либо как вносимые ЭДС +LiL(0) и
, либо как вносимые ЭДС +LiL(0) и  - в левой части, что чаще всего и делается.
- в левой части, что чаще всего и делается.
 … (3.1)
… (3.1)
 … (3.2)
… (3.2)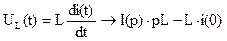 ,
,  .
.
 , то есть вносимые ЭДС отсутствуют.
, то есть вносимые ЭДС отсутствуют. .
.






