Порядок расчета. Операторный метод состоит из четырех этапов:
Операторный метод состоит из четырех этапов: 1 Расчет исследуемой цепи в установившемся режиме до коммутации (t≤ 0_) с целью определения независимых начальных условий, то есть токов в индуктивностях и напряжений на емкостях с последующим использованием их в расчете. 2 Перевод исследуемой электрической цепи в операторную форму (таблицы 3.1, 3.2). 3 Расчет полученной электрической цепи в операторной форме как обычной цепи постоянного или синусоидального в символической форме тока любым из известных методов (эквивалентные преобразования, законы Кирхгофа, узловые потенциалы и др.) с учетом того, что в расчете используются не реальные токи и элементы электрической цепи, а их операторные изображения в соответствии с приведенной здесь таблицей. 4 По найденным операторным изображениям искомых электрических величин определяются соответствующие им оригиналы. В принципе, нахождение оригиналов по их операторным изображениям может производиться по трем путям. Первый – по обратному преобразованию Лапласа. Этот путь достаточно сложен и в инженерных расчетах не используется. Второй – по таблицам оригиналов и изображений. Этот путь вполне приемлем и доступен для расчетов, но требует выполнения операции приведения полученного операторного изображения искомой функции к табличному виду. Несмотря на относительную простоту этой процедуры из школьной математической алгебры, в ряде случаев она может вызывать затруднения. Наиболее простым и часто употребляемым способом определения оригиналов является использование для этих целей теоремы разложения, в соответствии с которой: если операторное изображение искомой функции F(p) привести к виду правильной дроби Здесь р1, р2, р3, …, рn, …, рm – корни уравнения F2(p)=0. Понятно, что их количество определяется степенью полинома F2(p).
F1(pk), Сложность заключается только в том, что теорема разложения в приведенном здесь виде не может быть применена к вещественным и равным корням рk. Для случая вещественных и равных корней она существенно усложняется, что показано во всех учебниках по ТОЭ. Для наиболее распространенного случая двух корней р1 и р2 эти функции имеют вид: а) для пары вещественных и разных корней б) для пары вещественных и равных корней р12=р1=p2: Для определения функции-оригинала при двух попарно сопряженных комплексных корнях р1=(-δ +jω) и р2=(-δ -jω) формально теорема разложения используется в версии двух вещественных разных корней (а). При этом следует иметь в виду, что первое и второе слагаемые в (а) оказываются попарно сопряженными комплексными числами (функциями), то есть если При сложении мнимые составляющие, таким образом, взаимно уничтожаются. Это означает, что функция-оригинал находится как В случае расчета переходных процессов в цепях с синусоидальными ЭДС (или источниками тока) с предварительным переходом от ЭДС к их комплексным изображениям, результатом применения теоремы разложения будет комплексное изображение искомой величины, например, тока Функция-оригинал в этом случае есть коэффициент (функция) при мнимой части выражения В том случае, если один из корней полинома знаменателя р=р0=0, первое слагаемое в теореме разложения получает вид Детальное изложение теоремы разложения для всех видов электрических цепей с соответствующими доказательствами и обоснованиями приведено во всех учебниках курса ТОЭ.
|

 , где F1(p)=anpn+an-1pn-1+…+a1p+a0, F2(p)=bmpm+bm-1pm-1+…+b1p+b0 являются обычными линейными степенными полиномами (при n< m), что всегда возможно, то функция-оригинал
, где F1(p)=anpn+an-1pn-1+…+a1p+a0, F2(p)=bmpm+bm-1pm-1+…+b1p+b0 являются обычными линейными степенными полиномами (при n< m), что всегда возможно, то функция-оригинал 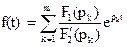 .
.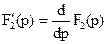 - производная полинома знаменателя, являющегося легко дифференцируемой степенной функцией.
- производная полинома знаменателя, являющегося легко дифференцируемой степенной функцией. ,
,  - значения соответствующих функций при р=рk. Результат вычисления состоит из простого сложения m экспоненциальных функций времени, что и составит функцию-оригинал.
- значения соответствующих функций при р=рk. Результат вычисления состоит из простого сложения m экспоненциальных функций времени, что и составит функцию-оригинал.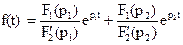 ;
; .
. , то
, то 

 .
. , то есть
, то есть  .
. .
.


