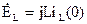О некоторых приемах упрощения расчета переходных процессов в операторной форме в цепях с синусоидальными ЭДС

 

В связи с тем, что операторное изображение синусоидальной функции является достаточно сложным и приводит к заметному усложнению расчетов, прибегают к приемам, исключающим необходимость использования операторного изображения синусоиды.

 

3.3.1 Первый способ состоит в том, что электрическая цепь с синусоидальными источниками ЭДС предварительно переводится в символическую форму, превращая их в функции времени с комплексными коэффициентами. При этом речь идет о переводе в комплексную форму всей синусоиды, то есть

.

Комплексные амплитуды здесь становятся обычными, не зависящими от времени постоянными коэффициентами. Такими же составляющими становятся и комплексные изображения параметров цепей R→ R, L→ jω L, .

Перевод в операторную форму комплексной версии цепи оказывается существенно более простым, приведенным в таблицах 3.1 и 3.2.

Особенностью здесь является необходимость перевода в символическую форму вносимых ЭДС, являющихся постоянными функциями времени (постоянными ЭДС).

Эта трудность легко преодолевается, так как любая функция f(t)=A=const может быть представлена как частный случай синусоиды:

.

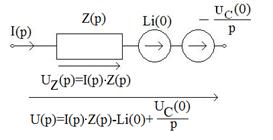
Здесь , то есть неизменяющаяся во времени функция может представляться как синусоида с частотой ω =0 и начальной фазой π /2.

Таким образом, комплексное изображение f(t)=A есть .

Это значит, что вносимая катушкой индуктивности постоянная ЭДС, равная L·i(0), в операторной форме должна быть представлена как , а вносимая ЭДС емкости как .

Результатом расчета в этом случае оказываются не реальные токи i(t) и напряжения U(t), а их комплексные изображения, от которых следует перейти к оригиналам.

3.3.2. Второй путь ухода от операторного изображения синусоиды состоит в сочетании классического и операторного методов.

Как известно, любой переходной процесс является следствием наложения двух режимов:

- принужденный режим после завершения переходного процесса, все электрические величины f_пр(t) в котором в цепях синусоидального тока являются синусоидами, получаемыми расчетом цепи в установившемся режиме, например, символическим методом без каких-либо ограничений;

- свободный режим, то есть собственно переходной процесс, происходящий в цепи при закороченных (удаленных из цепи) источниках сторонних сил (ЭДС), формируемый только под воздействием вносимых ЭДС, то есть энергий в катушках индуктивности и конденсаторах в момент коммутации. Этот свободный режим рассчитывается в операторной форме и таким образом находятся как операторные изображения, так и оригиналы f_св(t) всех составляющих свободный режим величин.

Окончательное решение представляется в виде f(t)= f_св(t)+f_пр(t).

Например, электрическая цепь с последовательным соединением R, L, C, питаемая от источника ЭДС е(t), в свободном режиме в операторной форме имеет вид, представленный на рисунке 3.4.

 

Рис. 3.4.

 

При этом следует иметь в виду, что токи и напряжения, включая начальные условия этих величин i_Lсв(0) и U_Cсв(0), относятся к свободному режиму, а это значит, что

i_Lсв(0)= i_Lсв(0)- i_Lпр(0) и U_Cсв(0)= U_Ссв(0)- U_Спр(0).

Рассматриваемая цепь в свободном режиме представляет собою неразветвленную электрическую цепь с двумя последовательно включенными в нее ЭДС Li_св(0) и . Операторное изображение тока в ней определяется с помощью закона Ома:

и окончательно i(t)= i_пр(t)+ i_св(t).

 

Таблица 3.1

Соответствие реальных функций и элементов электрических цепей их операторным изображениям

 

№	Область оригиналов / Элемент исходной схемы	Область изображений / Операторное изображение
	Постоянная ЭДС
	Синусоидальная ЭДС
	Резистор
	Индуктивность	4.1 i(0)=0 4.2 i(0)≠ 0
	Емкость	5.1 UC(0)=0     5.2 UC(0)≠ 0
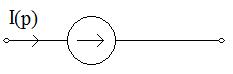
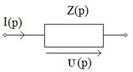	Обобщенный приемник электрической энергии	6.1 i(0)=0 и UC(0)=0 или , где 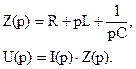6.2 i(0)≠ 0 и UC(0)≠ 0 или
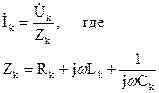
	Закон Ома для комплексных действующих значений напряжения и тока в обобщенном k–ом приемнике (в произвольной k–ой ветви)	Закон Ома для операторных изображений 7.1 i(0)=0 и UC(0)=0   7.2 i(0)≠ 0 и UC(0)≠ 0
	Первый закон Кирхгофа для комплексных действующих значений, сходящихся в k–ом узле	Операторная версия закона
	Второй закон Кирхгофа для комплексных действующих значений ЭДС и напряжений k–го контура	Операторная версия закона

 

Таблица 3.2

Операторные версии комплексных изображений постоянных и синусоидальных реальных и вносимых ЭДС

 

№	Функции-оригиналы	Комплексная версия	Операторные изображения
	Источник постоянной ЭДС e(t)=E=const	E(jω)=jE
	Источник синусоидальной ЭДС e(t)=Emsin(ω t+ψ e)
	ЭДС, вносимая начальным током iL(0) в катушке индуктивности EL=L·iL(0)
	ЭДС, вносимая начальным напряжением на конденсаторе EC=UC(0)