Порядок расчета.
1. Расчет переходных процессов целесообразно (но необязательно) начинать с расчета рассматриваемой цепи в установившемся режиме до коммутации, то есть при t£ 0_. Этот расчет позволяет найти значения токов и напряжений при t=0_, то есть в момент, непосредственно предшествующий коммутации. Интерес при этом представляют только токи в индуктивностях 2. Далее следует внимательно разобраться с конфигурацией цепи, получаемой после коммутации, определив наличие и количество в ней узлов, ветвей и контуров, выбрать метод расчета (законы Кирхгофа или метод контурных токов) и составить необходимое для решения количество (систему) дифференциальных уравнений. 3. Решение системы дифференциальных уравнений детально описано в предыдущем разделе. Если классический вариант решения не предписывается никакими условиями, следует приступить к формированию характеристического уравнения через входное сопротивление цепи в комплексной форме zвх(jw)→ z(p)=0 без решения составленной системы уравнений. Что касается составленных уравнений, они могут потребоваться для определения зависимых начальных условий и анализа работы цепи в послекоммутационном режиме. Порядок характеристического уравнения, как было показано, должен совпадать с количеством индуктивностей и емкостей в цепи. 4. Корни характеристического уравнения могут быть вещественными разными, вещественными равными и комплексными. При этом вещественные корни и вещественные составляющие комплексных корней должны быть отрицательными, а сами комплексные корни – попарно сопряженными. 5. Формирование функции свободной составляющей искомой электрической величины (iсв, Uсв) осуществляется в порядке, изложенном в предыдущем разделе. Для случая двух корней, скажем, для функции свободного тока, эти решения, как было показано, имеют вид:
6. Принужденная составляющая искомой функции определяется путем расчета исследуемой цепи в установившемся режиме после коммутации. 7. Общее решение (итоговая функция) искомой величины представляется в виде суммы Например, для тока при вещественных разных корнях эта функция будет иметь вид для двух вещественных одинаковых корней для комплексных 8. Определяются постоянные интегрирования (А1, А2, А, γ) с предварительным определением независимых (законы коммутации) и зависимых начальных условий (производных искомых функций при t=0). Например, для определения постоянных интегрирования, входящих в функцию тока при двух разных вещественных корнях необходимо иметь два уравнения (при t=0):
Из этих уравнений при известных i(0) и 9. Окончательное формирование функций искомой величины. 10. При необходимости определения функций других электрических величин пользуются или системой первоначально составленных уравнений, или соответствующими зависимостями между найденной и искомой величиной. Например, при найденном переходном токе i(t) первой ветви электрической цепи рисунка 2.1 переходное напряжение на резисторе находится по закону Ома
|

 и напряжения на емкостях
и напряжения на емкостях  , так как на основании законов коммутации только эти величины могут быть использованы для расчета цепи после коммутации при t≥ 0+.
, так как на основании законов коммутации только эти величины могут быть использованы для расчета цепи после коммутации при t≥ 0+. – для двух вещественных разных корней,
– для двух вещественных разных корней, – для двух вещественных равных корней,
– для двух вещественных равных корней, – для двух попарно сопряженных комплексных корней р1, 2 = –δ ±jw.
– для двух попарно сопряженных комплексных корней р1, 2 = –δ ±jw. .
. ,
, ,
,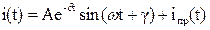 .
. .
. определяются А1 и А2.
определяются А1 и А2. , а на индуктивности – на основании того, что
, а на индуктивности – на основании того, что  .
.


