Таким образом, задача сводится к составлению и решению системы линейных дифференциальных уравнений, что и составляет и специфику, и основную трудность расчета
Как уже было показано, дифференциальные уравнения электрического состояния (равновесия) цепи можно составлять только или по законам Кирхгофа, или по методу контурных токов. При этом правила составления уравнений (как и формулировка законов) остаются традиционными с учетом лишь того, что связь между токами и напряжениями на элементах R, L и С представляется в виде:
Например, для цепи, представленной на рисунке 2.1,
Рис. 2.1
могут быть составлены следующие системы уравнений: – По законам Кирхгофа для реальных токов в ветвях i1, i2 и i3:
– По методу контурных токов (для контурных токов iI и iII):
Наиболее трудоемким этапом расчета является решение полученной системы уравнений и, прежде всего, приведение системы из нескольких уравнений к одному с одним неизвестным. В простейшем случае это делается методом последовательного исключения переменных, в других случаях путем алгебраизации дифференциальных уравнений [1, 2]. В случае цепи рисунка 2.1 приведение системы уравнений для двух контурных токов к одному может быть осуществлено следующим образом: – из первого уравнения находим ток – во втором уравнении освобождаемся от интеграла, дифференцируя левую и правую части – подставляя в полученное уравнение выражение для тока iII, после простых алгебраических преобразований получаем Это – неоднородное линейное дифференциальное уравнение второго порядка (с левой частью) с одним неизвестным iI. Его и следует решать. Получаемое таким образом уравнение в общем случае является неоднородным дифференциальным уравнением «n»-го порядка, решение которого, как известно из курса высшей математики, представляет собой сумму (наложение) частного решения неоднородного уравнения и общего решения однородного. Специфика решения системы дифференциальных уравнений, относящихся к задачам электротехники такова, что этот довольно сложный этап математического решения может быть заменен довольно простыми, вполне приемлемыми для инженерного решения задач, действиями. Дело в том, что решение неоднородного уравнения в задачах электротехники сводится к расчету уравнений электрического состояния (равновесия) цепи в установившемся режиме под воздействием действующих в цепи источников электрической энергии (левая часть уравнений). Поэтому этот режим часто называют принужденным (пр.) или установившимся (уст.). Этот режим может быть найден путем расчета цепи в установившемся после коммутации режиме любыми методами расчета электрических цепей. Это значит, что частное решение неоднородного уравнения, то есть принужденная составляющая переходного процесса, может быть найдено без составления и решения дифференциальных уравнений. Например, при синусоидальной ЭДС
В случае, если e(t)=E=const: Для получения общего решения однородного уравнения, то есть решаемого дифференциального уравнения, левая часть которого приравнивается к нулю, необходимо составить так называемое характеристическое алгебраическое уравнение и определить его корни. Характеристическое уравнение, как это следует из правил решения, формируется через алгебраизацию решаемого однородного уравнения путем замены в нем дифференциалов на некоторый оператор «р» в соответствующей степени Однородным уравнением, соответствующим найденному нами уравнению (5) является
Понятно, что исключение из уравнения левой части приводит к новому уравнению с иными переменными. Применительно к задачам электротехники это уравнение описывает работу цепи без влияния внешних (побуждающих) сил. Электромагнитные процессы в такой цепи происходят только под воздействием энергии, сосредоточенной в элементах L и C самой цепи. Этот режим называют свободным, а уравнение – уравнением для свободных составляющих токов iсв и напряжений Uсв, каковые и находятся в результате решения однородного уравнения. Характеристическое уравнение, соответствующее однородному уравнению (6) имеет вид
Однако при решении инженерных электротехнических задач составление характеристического уравнения может быть существенно упрощено. Оно может быть составлено без составления систем уравнений электрического состояния и математических операций с ними, которые, как мы видим, довольно не просты. Характеристическое уравнение любой цепи может быть получено из комплексной версии входного сопротивления рассматриваемой цепи Zвх (jw) при замене оператора «jw» на некоторый оператор «р» и приравнивании получаемого выражения Z(p) к нулю, то есть Z(p)=0. Например, характеристическое уравнение цепи рисунка 2.1 может быть получено путем составления Zвх (jw) со стороны зажимов источника:
Примечание: чрезвычайно важно помнить, что в выражении Zвх (jw) при всех математических операциях недопустимо отрывать символ «j» от «w», как недопустимо перемножать мнимые единицы. Поэтому сопротивление емкости следует записывать именно в виде Заменяя «jw» на «р», получаем
Приравнивая полученное уравнение к нулю, из Z(р)=0 получаем характеристическое уравнение цепи в виде:
Это уравнение полностью совпадает с только что найденным на основе правил решения дифференциальных уравнений. Понятно, что в инженерной электротехнической практике этот метод является наиболее эффективным. При этом следует хорошо понимать, что для любой конкретной цепи может существовать только одно характеристическое уравнение, не зависящее от того, для какой переменной (в цепи рисунка – для какого из токов i1, i2 или i3) оно составляется, то есть какие токи поэтапно исключаются в ходе решения. Итак, в конечном итоге проблема сводится к составлению и решению характеристического уравнения – обычного алгебраического уравнения, получаемого путем алгебраизации однородного дифференциального уравнения. Следует помнить, что порядок (степень) характеристического уравнения в электротехнических задачах всегда совпадает с количеством в рассчитываемой электрической цепи независимых, то есть не преобразуемых в эквивалентные накопителей электромагнитной энергии, к каковым относятся индуктивности и емкости. Например, цепь рисунка 2.1 имеет два накопителя (L1 и С3), что и приводит к характеристическому уравнению второй степени. Решение однородного уравнения никак не связано с побуждающими воздействиями, то есть не зависит от характера источников электрической энергии в цепи. В связи с этим режим, описываемый этим уравнением, называется свободным (св) и определяется только количественным и качественным составом элементов-накопителей электромагнитной энергии (L и С) и конфигурацией и составом элементов всей цепи. В одной и той же цепи при одних и тех же видах коммутации характер свободного режима одинаков как при постоянных, так и при синусоидальных ЭДС. В определенном смысле именно свободный режим и есть переходной процесс. При этом характер свободного режима, следовательно, собственно переходного процесса, определяется характером (видом) корней характеристического уравнения и принципиально имеет два вида, различных для вещественных и мнимых корней: – при вещественных корнях функции кривых токов и напряжений в электрических цепях имеют монотонный возрастающий или убывающий характер. В ряде случаев такие переходные процессы называют апериодическими, что не вполне корректно, так как периодических переходных процессов (переход цепи из одного установившегося режима в другой) принципиально быть не может. Для случая двух разных вещественных корней общим интегральным решением для свободного режима является экспоненциально изменяющаяся функция
Для случая двух равных вещественных корней эта функция приобретает иной вид, а именно
Здесь р1, р2 при р1=р2=р есть корни характеристического уравнения, а А1 и А2 – постоянные интегрирования. Внимание: в связи с тем, что переходные процессы, так или иначе, заканчиваются, вещественные корни характеристического уравнения всегда должны быть отрицательными, так что при t→ ∞ fсв(t)→ 0. Переходные процессы при двух одинаковых вещественных корнях иногда называют предельным случаем апериодического (правильнее – монотонно изменяющегося) переходного процесса. – При комплексных корнях переходной процесс в цепи носит апериодический колебательный характер. При этом: – вещественные части корней должны быть отрицательными; – все комплексные корни всегда должны быть попарно сопряженными. Для случая двух комплексных корней р1= –δ +jw, p2= –δ +jw (δ и w – произвольные числа, не имеющие отношения к часто обозначаемым этими буквами электрическим величинам), интегральное решение для свободного режима имеет вид Здесь δ и w – корни характеристического уравнения, а А и g – постоянные интегрирования. Таким образом, итоговые функции электрических величин переходного процесса (токи, напряжения) имеют вид: f(t)=fпр(t)+fсв(t). Здесь fпр(t) – принужденная составляющая переходного процесса, то есть тот режим, который устанавливается в цепи после коммутации и завершения переходного процесса, а fсв(t) – функция, определяющая переход цепи от установившегося докоммутационного режима к установившемуся послекоммутационному. Следующим этапом решения является определение значений входящих в f(t) постоянных интегрирования. В простейшем случае двух корней их всегда две (А1 и А2 или А и g). При решении линейных дифференциальных уравнений постоянные интегрирования, как известно, находятся исходя из начальных условий, то есть по значениям искомой функции f(t) или ее производных в момент t=0. Трудность заключается в том, что полученные в результате решения уравнений выражения для f(t) справедливы для периода 0+£ t£ ∞, то есть, начиная с момента после коммутации. Из докоммутационных начальных условий (t£ 0–), которые могут быть определены путем расчета цепи в установившемся режиме до коммутации, можно использовать только значения докоммутационных (при t=0–) токов в индуктивностях и напряжений на емкостях. Эти значения переносятся в послекоммутационный режим (при t=0+) на основании законов коммутации: iL(0–)=iL(0+) UС(0–)=UС(0+). Эти начальные условия называются независимыми и могут использоваться для вычисления постоянных интегрирования. Если независимых условий для этого недостаточно, необходимо определить дополнительные (зависимые) начальные условия, то есть производные i′ L(t) U′ C(t), каковыми фактически являются напряжения на индуктивности и ток в емкости. Как известно, напряжение на катушке индуктивности равно С другой стороны
|










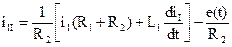 ;
; ;
;
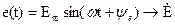 ток i(t) в общей ветви цепи рисунка 2.1 после завершения в ней переходного процесса может быть определен путем расчета этой цепи символическим методом:
ток i(t) в общей ветви цепи рисунка 2.1 после завершения в ней переходного процесса может быть определен путем расчета этой цепи символическим методом:
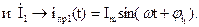
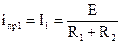 .
.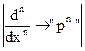 .
.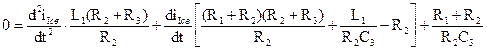
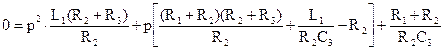 , которое после простых алгебраических преобразований приводится к
, которое после простых алгебраических преобразований приводится к , то есть к линейному алгебраическому уравнению второго порядка, решение которого сводится к определению его корней р1 и р2.
, то есть к линейному алгебраическому уравнению второго порядка, решение которого сводится к определению его корней р1 и р2. .
. , а не
, а не  .
.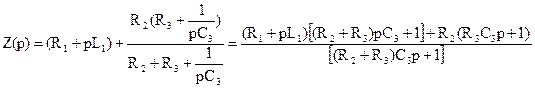 .
. .
. .
. .
. .
.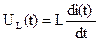 , откуда
, откуда 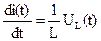 и при t=0
и при t=0 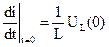 .
. , откуда
, откуда  и при t=0
и при t=0 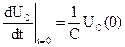 .
.


