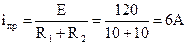Задача 1. Построить график зависимостей i=f(t) и u(t)
В схеме рисунка 1.1: Е=120 В, R1=R2=10 Ом, L=10 мГ. Определить токи в цепи после замыкания ключа К. Построить график зависимостей i=f(t) и u(t).
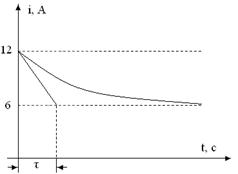
Рисунок 4.1 Решение. 1. Рассчитываем цепь в установившемся режиме до коммутации (при t£ 0_). При разомкнутом ключе К цепь представляет из себя один контур с последовательным соединением R1, L и R2. При Е=const ток в цепи будет постоянным, а L – есть обычный проводник без сопротивления. Значит, i(t£ 0_)=I=E/(R1+R2)=120/(10+10)=6A. Отсюда следует, что i(0_)=6 А. 2. Выполняем коммутацию (замыкаем ключ). Совершенно ясно, что после коммутации мы будем иметь две фактически независимые друг от друга цепи: - одноконтурная цепь с последовательным соединением Е, R1 и L, а также - одноконтурная замкнутая цепь с сопротивлением R2 без источника. Поскольку во второй цепи накопители энергии (индуктивность, емкость) отсутствуют, переходного процесса в ней не будет и ток в R2 исчезнет мгновенно. Значит, переходной процесс будет иметь место только в первой цепи, для расчета которой достаточно уравнения по второму закону Кирхгофа: 3. К одному уравнению с одним неизвестным оно приводится путем выражения каждого из слагаемых правой части через ток. В результате этих действий получаем неоднородное дифференциальное уравнение Уравнение имеет первый порядок, что соответствует одному накопителю энергии в цепи (индуктивность). 4. Решение такого уравнения состоит из суммы решений в переходном свободном и установившемся (принужденном) режиме после коммутации (при t≥ 0+), то есть i(t)=iсв(t)+iпр(t). 4.1. Дифференциальное уравнение для свободного режима (исходное уравнение без правой части) 4.2. Соответствующее этому уравнению характеристическое – линейное алгебраическое уравнение первой степени Кстати, это уравнение полностью совпадает с тем, которое может быть получено из выражения для входного сопротивления в комплексной форме цепи после коммутации Z=R1+jwL после замены jw на р и приравнивания получаемого выражения к нулю Z(р)=R1+рL=0. 4.3. Таким образом, здесь мы имеем один действительный отрицательный корень Значит, ток свободного режима iсв=Аерt=Ae-1000t. 4.4. Рассчитывая цепь в установившемся режиме после коммутации, находим принужденную составляющую тока 4.5. Таким образом, общий ток после коммутации i(t)=iпр(t)+iсв(t)=12+Ае-1000t. 4.6. Ясно, что для определения одной постоянной интегрирования А достаточно иметь одно начальное условие, а именно i(0+). В соответствии с первым законом коммутации i(0+)= i(0_)=6А. 4.7. Определяем постоянную интегрирования А: i(0)=12+A=6, A=-6. 4.8. Записываем окончательное выражение для тока и переходного процесса i=12-6e-1000t. По полученному уравнению для тока строим график i=f(t).
Рисунок 4.2
5. Характер изменения напряжений на R1 и L, если это необходимо, определяется следующим образом:
6. Таким образом, ток в цепи без скачков изменяется от установившегося докоммутационного (6 А) до установившегося послекоммутационного (12 А) по экспоненте с постоянной времени Напряжение на активном сопротивлении в измененном масштабе повторяет кривую тока, изменяясь от 60 В ( Напряжение на индуктивности в момент коммутации скачкообразно возрастает от нуля до 60 В, а затем по экспоненте с постоянной времени τ =0, 001с уменьшается до нуля. Соответствующие кривые имеют вид, представленный на рисунке 1.3.
Рисунок 4.3.
Задача 2. Решить предыдущую задачу для случая размыкания ключа К. построить график зависимости i=f(t). Решение. Задача решается без соблюдения рекомендованной последовательности действий. 1. Записываем дифференциальное уравнение на основании закона Кирхгофа для момента времени после коммутации:
2. Представляем искомый ток в виде суммы свободной и принужденной составляющих: i=iпр+iсв 3. По любому из методов составляем характеристическое уравнение и находим его корни: R1+R2+pL=0
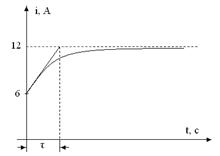
4. Решение для свободного тока ищем в виде iсв=Ae-2000t 5. Определяем принужденную составляющую искомого тока переходного процесса
6. На основании первого закона коммутации находим значение тока переходного процесса в момент t=0
7. Рассчитываем постоянную интегрирования А i(0)=6+А=12А, А=6А 8. Записываем окончательное выражение для тока переходного процесса i=6+6е-2000t 9. По полученному уравнению для тока i строим график
Рис. 4.4
|
.
.
.
.
.
.
,
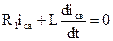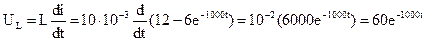или
.
.
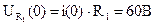) до 20 В (
).
