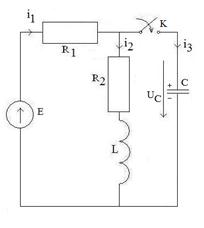
Задача 5. Рассчитать переходной процесс в цепи рисунка 5.1, если Е=60 В, R1=400 Ом, R2=800 Ом, L=0.2 Гн, С=2,5 мкФ
Рассчитать переходной процесс в цепи рисунка 5.1, если Е=60 В, R1=400 Ом, R2=800 Ом, L=0.2 Гн, С=2, 5 мкФ.
Рис. 4.9 Предполагается при этом, что к моменту коммутации напряжение на конденсаторе составляло U(t≤ 0_)=20 В. 1. Расчет цепи в установившемся режиме до коммутации и определение независимых начальных условий при t=0_. В связи с тем, что E=const, катушка индуктивности представляет собою обычное короткое замыкание на соответствующем участке, а ветвь с емкостью разомкнута, UС(0_)=20 В (по условию). 2. Замыкаем цепь с емкостью, выбираем метод расчета и составляем необходимое количество уравнений. Как известно, расчет цепи в случае несинусоидальных непериодических токов и напряжений может производиться либо с помощью законов Кирхгофа, либо методом контурных токов. После коммутации мы имеем дело с цепью, состоящей трех ветвей и двух ячеечных контуров. При расчете цепи по законам Кирхгофа составляются три уравнения i1-i2-i3=0 E=UR1+UR2+UR3=i1R1+i2R2+L E=UR1+UC=i1R1+ Формально более экономичным здесь является метод контурных токов. При условии, что контурный ток первого контура iI=i1, а второго iII=i3, составляются два следующих уравнения:
При этом следует иметь в виду, что уравнения Кирхгофа являются более универсальными и часто оказываются более полезными при дальнейших расчетах. 3. Приведение системы уравнений к одному с одним неизвестным. Эта процедура выполняется методом подстановок (поэтапное исключение переменных), либо методом алгебраизации, подробно рассмотренных в [1], [2]. Опуская довольно длительные, связанные с такими преобразованиями действия, приводим их конечный результат – итоговое линейное дифференциальное уравнение второго порядка:
4. Решение полученного уравнения. Как известно, применительно к задачам электротехники решение линейного дифференциального уравнения состоит из двух слагаемых искомой величины: свободной (св.) и принудительной (пр.). В данном случае i3=i3св+i3пр. 4.1. Определение свободной составляющей. Свободная составляющая есть результат решения однородного дифференциального уравнения для свободного режима, то есть итогового уравнения без правой части
Соответствующее характеристическое уравнение имеет вид
R1CLp2+(L+R1R2C)p+(R1+R3)=0 Гораздо более экономным и приемлемым для инженерной практики методом получения характеристического уравнения является вариант использования для этого выражения входного сопротивления цепи в комплексной форме. В нашем случае
При jω → p При Z(p)=0 получаем ранее полученное характеристическое уравнение R1CLp2+(L+R1R2C)p+(R1+R2)=0 4.2. Определение корней характеристического уравнения и составление функции для свободной составляющей. Подставляя в полученное уравнение значения составляющих его величин, получаем 2·10-4р2+р+1200=0. В этом случае мы имеем р1=-2000С-1 р2=-3000С-1 То есть два равных отрицательных вещественных корня. Свободная составляющая для тока в этом случае представляется в виде суммы двух экспонент iсв= Поскольку характеристическое уравнение для одной и той же цепи всегда только одно, корни характеристического уравнения, следовательно – вид функций для свободных составляющих всех электрических величин, определяющих функционирование цепи, будет иметь один и тот же вид, то есть: i1св= i2св= i3св= ULсв= UCсв= Разными здесь оказываются только постоянные интегрирования, определяемые по значениям соответствующих начальных условий. 4.3. Расчет цепи в после коммутационном установившемся режиме и определение принужденной составляющей. В установившемся режиме после коммутации мы снова имеем дело с цепью постоянного тока, когда емкость представляет собою разрыв цепи, а индуктивность – короткое замыкание. Это означает, что i1пр=i2пр=i=I=E/(R1+R2)=0, 05 A i3пр=0, ULпр=0, UCпр=i2R2=IR2=40 B. 4.4. Составление итоговой функции искомой (искомых) величины. Каждая из таких функций есть сумма принужденной (послекоммутационной) и свободной составляющих, то есть i1= i1пр+i1св=0, 05+ i2= i2пр+i2св=0, 05+ i3= i3пр+i3св= ULсв= ULпр+ULсв= UCсв= UCпр+UCсв=40+ Поскольку вещественные корни характеристического уравнения (всегда) отрицательны, свободные составляющие имеют затухающий характер и после завершения переходного процесса все электрические величины в цепи становятся равными принужденным составляющим. 4.5. Определение постоянных интегрирования. Этот этап расчета начинается с выбора электрической величины, которая при расчете представляет наибольший интерес. Предположим, что нас интересует, прежде всего, переходной ток в катушке индуктивности, то есть i2= Для определения постоянных интегрирования необходимо составить два уравнения с их участием. В соответствии с правилами высшей математики в данном случае такими уравнениями являются значения искомого переходного тока и его производной в начальный момент времени после коммутации, то есть при t=0+. Первое уравнение i2(0)= Второе уравнение
Значение первой производной тока определяется из того, что Значение UL(0) относится к зависимым начальным условиям и определяется из первоначально составленных для расчета данной цепи уравнений, записываемых для t=0, то есть i1(0)-i2(0)-i3(0)=0 E(0)=UR1(0)+UR2(0)+UL(0)=i1(0)R1+ i2(0)R2+UL(0) E(0)=UR1(0)+UС(0)=i1(0)R1+UС(0) Подставляя в эту систему известные величины и найденные независимые начальные условия, получаем i1(0)-0, 05-i3(0)=0 60= i1(0)·400+ 0, 05·800+UL(0) 60=i1(0)·400+20 Таким образом i1(0)=(60-20)/400=0, 1 А UL(0)=60-0, 1·400-0, 05·800=-20 Следовательно, второе уравнение для определения постоянных интегрирования имеет вид: -20=0, 2(-2000В1-3000В2) Решая это уравнение в системе с первым, получаем: В1=-0, 1, В2=0, 1. Окончательная функция переходного тока в индуктивности i2=0, 05-0, 1е-2000t +0, 1е-3000t. Для определения остальных электрических величин можно было бы воспользоваться выражениями для них п. 3.4.4 через определение их постоянных интегрирования в соответствии с п. 3.4.5. Но гораздо проще сделать это, воспользовавшись составленной в начале расчета общей системой уравнений электрического состояния рассматриваемой цепи (п. 2). Например, общий ток i1(t) – из уравнения 3.2.2:
Ток в ветви с емкостью может быть найдет из уравнения 3.2.1: i 3=i1-i2=0, 2e-2000t-0, 15e-3000t. При этом
5. Анализ поведения электрических величин в переходном режиме обычно сводится к построению кривых интересующих величин, определению характера и длительности переходного процесса, к анализу энергетических взаимодействий в рассматриваемой цепи. В качестве примера на рисунках 5.2 и 5.3 приведены последовательности построений (качественно) и результирующие кривые переходного тока в индуктивности i2(t) и переходного напряжения на емкости UС(t).
Рис. 4.10
Рис. 4.11
|

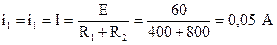 .
.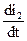
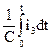 +A
+A

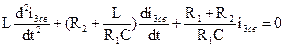
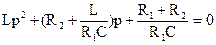 , то есть
, то есть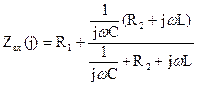

 .
. ,
, ,
,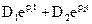 ,
, .
.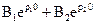 =В1+В2.
=В1+В2.
 , откуда
, откуда 
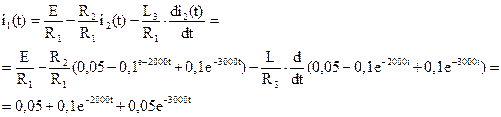
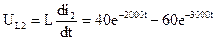 ,
,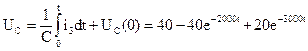 .
.




