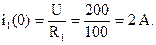Задача №1. В представленной здесь цепи U=200 В, R1=100 Ом, R2=400 Ом, С=5 мкФ
В представленной здесь цепи U=200 В, R1=100 Ом, R2=400 Ом, С=5 мкФ. Найти функцию входного переходного тока i1(t).
Рис. 4.18
Решение 1. Рассчитываем цепь до коммутации и определяем независимые начальные условия, в данном случае UС(0_). Понятно, что UС(0_)= UС(0+)=0. 2. Переводим цепь в операторную форму (таблица 3.2):
Рис. 4.19 Здесь U(p)= Z1(p)=R1=100 Z2(p)=R2=400 Z3= 3. Рассчитываем полученную цепь с помощью эквивалентных преобразований
Это выражение полностью соответствуют теореме разложения. Здесь F1(p)=0, 4p+200 F2(p)=0, 2p2+500p 4. Определяем оригинал входного тока
4.1. Находим корни полинома знаменателя F2(p)=0: р1=0, р2=-2500. 4.2. Находим производную полинома знаменателя:
4.3. Формируем функцию-оригинал: F1(p1)=F(0)=0, 4·0+200=200 F1(p2)=0, 4·(-2500)+200=-800 F′ 2(p1)= F′ 2(0)=0, 4·0+500=500 F′ 2(p2)=0, 4·(-2500)+500=-500
Проверка решения: t=0→ i1(0)=0, 4+1, 6=2 A Это решение верно, так как UC(0_)=UC(0+)=0, а при нулевых начальных условиях емкость – короткое замыкание. Это значит, что в момент коммутации сопротивление R2 шунтируется (замыкается накоротко) емкостью, то есть эквивалентное входное сопротивление цепи при t=0 равно R1 и t→ ∞ → i1(t)=0, 4 A. Это решение верно, так как при установившемся режиме емкость – разрыв цепи и сопротивление току равно R1+R2=500 Ом, поэтому
|






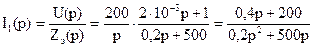

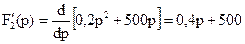 .
.