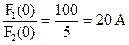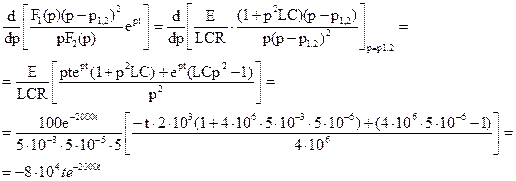Задача №4. Определить ток i(t) переходного процесса в схеме рис
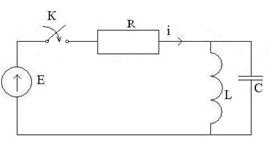
Определить ток i(t) переходного процесса в схеме рис. 4.1. Дано R=5 Ом, L=5·10-3 Гн, С=5·10-5 Ф, Е=100 В.
Рис. 4.24 Решение 1. Расчет цепи до коммутации приводит к тому, что iL(0_)=iL(0+)=0, UC(0_)=UC(0+)=0. Это значит, что вносимые этими элементами в момент коммутации ЭДС отсутствуют, и операторное изображение цепи представляется в виде схемы рис. 4.2.
Рис. 4.25
Здесь 2. Рассчитываем полученную цепь как обычную цепь постоянного тока при одном источнике методом эквивалентных преобразований.
Здесь F1(p)=E(1+LCp2),
3. Находим корни знаменателя F2(p)=0→ р0=0, р1=р2=-2000С-1. Таким образом, полином знаменателя имеет один нулевой и два кратных вещественных отрицательных корня. 4. Теорема разложения для этого случая имеет вид:
В нашем случае F1(p)=E(1+LCp2) F2(p)=LCR(p2+ Для нулевого корня р(0)=0 F1(0)=E, F2(0)=R, Для кратных корней р1, 2=-2000с-1
5. Записываем окончательное выражение для искомого тока переходного процесса i(t)=20-8·10-4te-2000t 6. Проверка решения При t=0 I(0)=20 А При t=∞ I(∞)=20 А Что соответствует физическому смыслу схемы рис. 4.1.
|
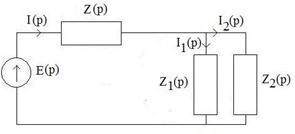
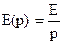, Z(p)=R, Z1(p)=Lp, Z2(p)= 
.
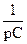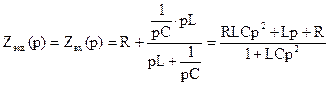и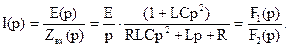
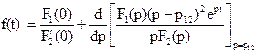, где р12=р1=р2=-2000С-1.
)
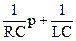