Задачи для самостоятельного решения. 1. Рассчитать классическим и (для сравнения) операторным методом переходный процесс в цепи с индуктивностью
1. Рассчитать классическим и (для сравнения) операторным методом переходный процесс в цепи с индуктивностью, приведенной ниже, и определить мгновенные значения напряжений uR1(t) и uRL, показанные на схеме, после замыкания ключа S. Параметры элементов схемы имеют значения: R1=R2=100 Ом, L=0, 1 Гн. Напряжение источника Е=100 В. Построить графики временных зависимостей этих напряжений.
2. Вычислить uR1(t) и uRC после замыкания ключа S в схеме, изображенной ниже. Параметры элементов схемы имеют следующие значения: R1=R2=500 Ом, С=2 мкФ. Напряжение источника Е=50 В.
3. В схеме, изображенной ниже, имеются два ключа S1 S2, с помощью которых производится коммутация обмотки реле с параметрами Rk, Lk. Первый ключ S1 замыкается в момент времени t1=0, в результате чего по обмотке реле возникает ток. Второй ключ S2 замыкается через интервал времени t2=0, 5 мс после замыкания ключа S1. Требуется определить время ТC срабатывания реле, если его ток срабатывания составляет IC=1 А. параметры элементов схемы имеют значения: R1=Rk=50 Ом, Lk=50 мГн, Е=100 В.
4. Определить i1(0+), i2(0+) и i3(0+), если R1=10 Ом, R2=10 Ом, R3=20 Ом, U=120 В, а UC(0_)=60 В.
5. Определить возникающие в цепи после коммутации токи i(t), i1(t), i2(t) и напряжение UC(t), если U=120 В, R=10 Ом, С=100 мФ.
6. В приведенной схеме R1=2 Ом, R2=2 Ом, L=0, 0096 Гн, ω =314 рад/с. Определить функцию i(t).
7. Схеме цепи после коммутации соответствует операторная схема замещения
8. При полностью заряженном конденсаторе схеме цепи после коммутации соответствует операторная схема замещения
9. Определите функцию переходного напряжения на конденсаторе (классическим и операторным методом). E=200 В, R1=100 Ом, R2=400 Ом, C=5 мкФ.
10. Определите ток i(t) переходного процесса на входе представленной здесь электрической цепи. E=100 В, R=5 Ом, L=5·10-3 Гн, C=5·10-5 Ф.
11. Определить ток переходного процесса в неразветвленной части цепи.
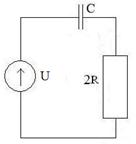
12. Определить переходной ток в цепи, если Расчет произвести всеми известными методами, в том числе используя классический метод для вычисления принужденного тока iпр(t) и операторный – для определения свободной составляющей iсв(t).
Ответы на задачи для самостоятельного решения
1) UR1(t)=50(1-e-2000t) UR2L(t)=50(1+e-2000t)
2) UR1(t)=25e-500t UR2C(t)=50-25e-500t
3) TC=0, 8c
4) i1(0)=3 A, i2(0)=3 A, i3(0)=0
5)
6) i=35, 2sin(314t-106°20′)-8, 4е-210t 7) 4 8) 2 9) UC(t)=160(1-e-2500t) 10) i(t)=20-8·104te-200t 11) i(t)=6, 16·10-3sin(314t+23°28′)-0, 054·10-3e-20t-2, 4·10-3e-2500t 12) iпр(t)=0, 472sin(400t-180°) i св(t)=0, 282e-25tsin(315t+72°30′) i(t)= iпр(t)+ iсв(t)
Рекомендуемая литература
1. Теоретические основы электротехники: Учебник для студентов вузов. Т.2/ К.С. Демирчан, Л.Р. Нейман, Н.В. Коровкин, В.Л. Чечурин. ─ 4-е изд. ─ СПб.: Питер, 2007. ─ 575с.: ил. 2. Бессонов, Л.А. Теоретические основы электротехники. Электрические цепи: Учебник для вузов — Изд. 11-е, испр. и доп. — М.: Гардарики, 2007. — 701с.- 25 экз. 3. Атабеков, Г.И. Теоретические основы электротехники. Линейные электрические цепи: учеб. пособие — Изд. 8-е, стер. — СПб.: Лань, 2010. — 592 с. - 5 экз.
4. Фриск В.В. Основы теории цепей: Учеб. пособие/ В.В. Фриск. ─ М.: ИП РадиоСофт, 2002. ─ 288с.: ил.
5. Кагаков Ю.Н., Расчет и анализ нелинейных электрических цепей в переходных режимах, АГТУ, Астрахань, 2005, 70с.
|


















 R1=50·103 Ом, L1=20 Гн, C2=6·10-6 Ф, R2=10·103 Ом.
R1=50·103 Ом, L1=20 Гн, C2=6·10-6 Ф, R2=10·103 Ом.
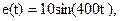 R1=10 Ом, R2=5 Ом, L=0, 1 Гн, C2=100 мкФ.
R1=10 Ом, R2=5 Ом, L=0, 1 Гн, C2=100 мкФ.




