Задача 7. Найти токи переходного процесса в электрической цепи (рис
Найти токи переходного процесса в электрической цепи (рис. 7.1), если Е=100 В, R1=R2=50 Ом, L=0, 125 Гн, С=180 мкФ.
Рис. 4.13
Принципиально решение этой задачи ничем не отличается от решения предыдущей, как и любой другой, и может быть выполнено в строго той же последовательности. Тем не менее, решение этой и других задач приводится в экспресс-варианте без повторения ранее приведенных комментариев и уже обсужденных подробностей с тем, чтобы дать повод для самостоятельных поисков и размышлений.
Решение 1. Предоставляем токи переходного процесса в виде двух составляющих – принужденной и свободной, то есть i(t)=iпр(t)+iсв(t) 2. Находим корни характеристического уравнения Z(p)=0
LCR1p2+(R1R2C+L)p+R1+R2=0 p2+510p+8, 88·104=0 p1, 2=-225±j155C-1=-β ±jω 0 Таким образом, единственным отличием при решении этой задачи от предыдущей является то, что здесь мы имеем не вещественные, а два комплексных сопряженных корня с отрицательной вещественной частью. Свободная составляющая тока как результат решения дифференциального уравнения в этом случае имеет вид: iсв(t)=Ае-β tsin(ω 0t+φ)=Ае-225tsin(155t+φ), где А и φ есть постоянные интегрирования, определение которых производится точно так же, как и в предыдущей, и во всех других задачах. 3. Решение токов переходного процесса ищем в виде i(t)=iпр(t)+ Ае-β tsin(ω 0t+φ) 4. Находим принужденные составляющие токов и напряжения на конденсаторе
5. Находим значение всех токов переходного процесса при t=0 на основании законов коммутации UC(0_)=UC(0)=E=50 B i2(0_)=i2(0)=0
i3=i1(0)-i2(0)=0-0=0 6. Находим первые производные всех токов при t=0, для чего составим дифференциальные уравнения: R1i1+UC=E
i1=i2+i3
7. Рассчитываем постоянные интегрирования
Так как
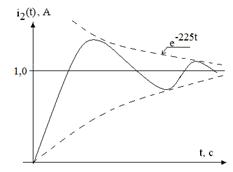
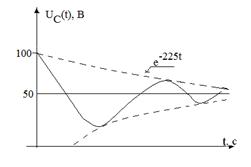
8. Выражения для токов переходного процесса имеют вид i1(t)=1, 761e-225tsin(155t+34, 6°) i2(t)=1+3, 864e-225tsin(155t-15°) i3(t)=-5, 161e-225tsin155t Выражения для напряжений на индуктивности и емкости, если это требуется, могут быть определены, как Таким образом, в этом случае (при комплексных корнях) мы имеем дело с колебательным переходным процессом. Характер изменения (качественно) приобретает вид, представленный на рисунках 7.2 и 7.3 (сравнить с 1.2 и 1.3).
Рис. 4.14
Рис. 4.15
|



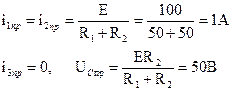
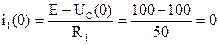
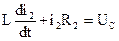
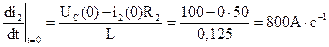
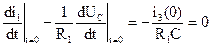


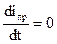 , то
, то
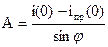 ,
, 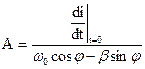

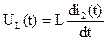 и
и  .
.