Задача 8. Определить ток переходного процесса в электрической цепи (рис
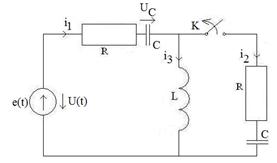
Определить ток переходного процесса в электрической цепи (рис. 8.1) после размыкания ключа К, если U(t)=100sin(1000t+π /4), R=10 Ом, С=100 мкФ, L=10 Гн.
Рис. 4.16
Решение 1. Рассчитываем цепь в установившемся режиме до коммутации. Здесь мы имеем дело с одним источником ЭДС. Расчет проводим методом эквивалентных преобразований в символической форме (рис. 8.2).
Рис. 4.17
Комплексная амплитуда общего тока
Комплексная амплитуда тока индуктивности
Комплексная амплитуда напряжения на емкости
Следовательно, до коммутации UС(t)=50sin(1000t-π /4) и UС(0_)=-50sinπ /4=-25 Напряжение на емкости С в параллельной ветви нас не интересует, поскольку эта емкость никакого влияния на переходной процесс после коммутации не оказывает. 2. Составляем характеристическое уравнение по входному сопротивлению цепи после коммутации.
Следовательно, характеристическим уравнением цепи является RpC+p2LC+1=0 или p2+103p+106=0. Отсюда 3. Таким образом, решение для свободного тока ищем в виде iсв=Ae-500tsin(500 4. Находим принужденную составляющую тока переходного процесса
Значит iпр=10sin(1000t+π /4). 5. Таким образом, общая функция переходного тока имеет вид i=iпр +iсв=10sin(1000t+π /4)+ Ae-500tsin(500 6. Определяем постоянные интегрирования Первым уравнением для определения постоянных интегрирования является i3(0+)= i3(0_)= i(0+)=10sin π /4+Аsin ψ =5 Для получения второго уравнения следует найти значение его производной при t=0
Значение этой производной при t=0 находим из уравнения электрического состояния цепи (Кирхгофа) после коммутации, то есть U(t)=iR+UC+L
Таким образом, вторым уравнением для определения А и ψ является 5·103+А·500cosψ -A·500·sinψ =75 Решение этих уравнений дает
7. Записываем окончательное выражение для тока переходного процесса
При необходимости определения функций UL(t) и UC(t) после коммутации можно воспользоваться
При качественном построении графиков итоговых функций следует понимать, что здесь происходит вычитание из значений в каждый момент времени установившейся синусоиды значений экспоненциально убывающей синусоиды. При этом речь идет о синусоидах разных частот. Затухание второй синусоиды происходит с постоянной времени
|


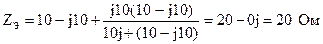

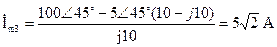 , то есть i3=5
, то есть i3=5 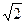 sin103t, i3(0_)=0.
sin103t, i3(0_)=0.

 .
.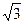 t+ψ)
t+ψ)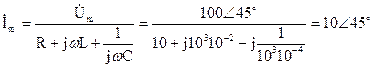
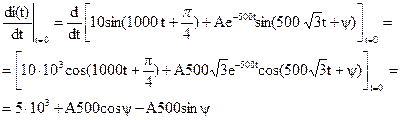
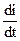 , откуда
, откуда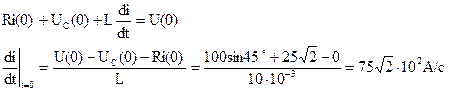
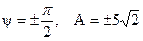 . Принимаем
. Принимаем 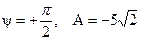

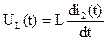 и
и 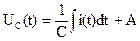 .
.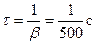 . Через (4÷ 5)τ можно считать, что в составе тока останется только принужденная составляющая.
. Через (4÷ 5)τ можно считать, что в составе тока останется только принужденная составляющая.


