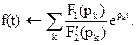Задача №2. Определить ток в индуктивности (рис
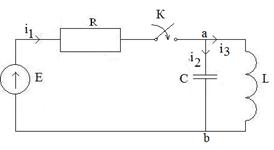
Определить ток в индуктивности (рис. 2.1) после замыкания ключа «К». Дано: R=250 Ом, С=2 мкФ, L=667 мГ, Е=125 В.
Рис. 4.20
Решение 1. Рассчитываем заданную цепь до коммутации (ключ К разомкнут). Понятно, что в этом случае iL(0_)=0 и UC(0_)=0 (конденсатор в установившемся режиме шунтируется катушкой). 2. Переводим цепь в операторную форму по правилам таблицы 3.2:
Рис. 4.21
Здесь 3. Рассчитываем полученную цепь как обычную цепь постоянного тока, воспользовавшись правилом определения тока в одной из двух параллельных ветвей (метод эквивалентных преобразований):
Таким образом, мы получили выражение для I3(p) в виде, который для определения оригинала позволяет воспользоваться теоремой разложения в общепринятой версии
Здесь F1(p)=125, F2(p)=p(RLCp2+Lp+R)=RLCp3+Lp2+Rp=p(3, 333·10-4p2+667·10-3p+250), pk – корни полинома знаменателя F2(p)=0, F′ 2(p) – производная полинома знаменателя. 4. Последовательность действий при определении функции-оригинала i3(t): 4.1. Определяем корни многочлена знаменателя: р0=0, р1=-500С-1, р2=-1500С-1. 4.2. Находим производную полинома знаменателя:
4.3. Для трех вещественных и разных корней (равенство нулю одного из них в данном случае значения не имеет) теорема разложения имеет следующий вид:
Поскольку F1(p)=125 – не зависит от р, имеем F1(p1)=F1(p2)=F1(p3)=F1(0)=125. Значения производной знаменателя в точках р1, р2 и р3:
Таким образом
4.4. Окончательное выражение для тока в индуктивности имеет вид
5. Если кроме найденной функции, в данном случае тока i3(t), требуется найти переходные функции других электрических величин исследуемой цепи, это можно выполнять как в области операторных изображений с последующим переходом к оригиналам, так и оперируя с найденными функциями-оригиналами. Например, для определения переходной функции напряжения на конденсаторе UC(t) в первом случае действуют по схеме: I3(p)→ Uab(p)=I3(p)Z3(p)=I3(p)·pL→ Uab(p)=UC(p) → UC(t). Во втором случае решение окажется чрезвычайно простым:
|

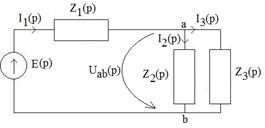
 , Z1(p)=R, Z2(p)=
, Z1(p)=R, Z2(p)= 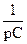 , Z3(p)=pL, а вносимые ЭДС в ветвях с емкостью и индуктивность отсутствуют, так как i3(0+)=0 и UC2(0+)=0.
, Z3(p)=pL, а вносимые ЭДС в ветвях с емкостью и индуктивность отсутствуют, так как i3(0+)=0 и UC2(0+)=0.