Задача №6. Пользуясь теоремой разложения, определить ток переходного процесса в неразветвленной части цепи (рис
Пользуясь теоремой разложения, определить ток переходного процесса в неразветвленной части цепи (рис. 6.1). Дано R1=50·103 Ом, R=10·103 Ом, L=20 Гн, С=6·10-6 Ф, U(t)=
Рис. 4.28 Решение 1. Здесь мы имеем нулевые начальные условия, поэтому вносимые ЭДС отсутствуют. 2. На основании закона Ома записываем уравнение искомого тока в операторной форме
Напряжение источника в операторной форме имеет вид:
Поэтому
3. По теореме разложения найдем оригинал
Из условия F2(p)=0 находим корни p1=jω =314jc-1 p2·20·104·6·10-6+p(20+50·103·10·104·6·10-6)+80·103=0 1, 2p2+3020p+6·104=0
p2=-20c-1, p3=-2500c-1 F′ 2(p)=p2RLC+p(L+R1RC)+R1+R+(p-j)(2pRLC+L+R+R1) F′ 2(p1)=(314j)2·1, 2+j314·3020+6·103=-95·104 F′ 2(p2)=(-20-314j)[(-20) ·2, 4+3020]=-93, 5·104 F′ 2(p3)=(-2500-314j)[(-2500) ·2, 4+3020]=-93, 5·104 F1(p)=Um(1+RCp) F1(p1)=220 F1(p2)= -220 F1(p3)= -220 4. Записываем уравнение для искомого тока в комплексной форме
5. Переходя от комплексной формы к действительной, получим окончательное уравнение для тока переходного процесса i(t)=6, 16·10-3sin (314t+230891)-0, 054·10-3e-20t-2, 4·10-3e-2500t 6. Проверка правильности решения При t=0 i(0)=0 i(0)=2, 4538-0, 054-2, 4=0
|
.
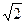+18, 87 
