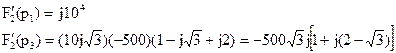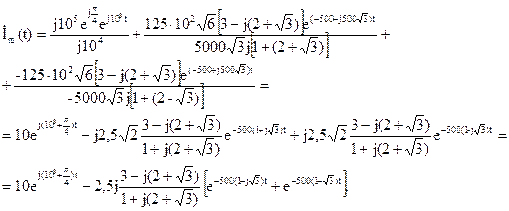Задача №5. Пользуясь операторным методом определить ток переходного процесса в цепи рис
Пользуясь операторным методом определить ток переходного процесса в цепи рис. 5.1 после размыкания ключа К. Дано iL(0)=0, UС(0)=-25
Рис. 4.26 Решение 1. Расчет цепи до коммутации, который в данном случае целесообразно было бы произвести в символической форме, здесь не нужен, ибо ток в индуктивности iL(0)=0 и напряжение на емкости UС(0)=-25 2. Переводим заданную цепь в операторную форму (рис. 5.2), предварительно перейдя от реальных функций ЭДС источника и вносимой емкостью ЭДС к их комплексным изображениям:
Рис. 4.27
U(t)=e(t)=Umsin(ω t+ψ)→ Umejψ ejω t= = UC(0) → jUC(0) → j Здесь Um=100 В, ψ =π /4, ω =103 c-1 3. Рассчитываем полученную операторную схему с помощью закона Ома (последовательное соединение двух источников и трех приемников):
4. Записываем уравнение для искомого тока на основании исходной формы теоремы разложения и находим его элементы, учитывая то, что в этом случае в качестве оригинала выступают не сами функции, а их комплексные изображения:
Полином знаменателя здесь имеет три корня р1=103j, р2, 3=-500±j500 4.1. Находим значения полинома числителя при р1, р2, р3.
4.2. Находим производную полинома знаменателя
и ее значения при р=р1 и, например, при р=р3:
5. Записываем искомый ток переходного процесса в комплексной форме
6. Беря мнимую часть от полученного уравнения в комплексной форме, найдем окончательное выражение для искомого тока в функции времени Имеем
|
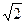B, R=10 Ом, L=10-2 Гн, С=10-4 Ф, U(t)=100sin(103t+ 
).
.
.
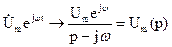
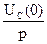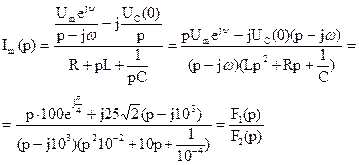
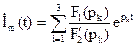
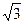