Общая идея метода факторного анализа
Тем или иным способом формулируется представление о том, что требуется для того, чтобы система исходных параметров считалась хорошо представленной с помощью системы факторов. Для этого строится критерий (иногда последовательность критериев), значение которого можно определить, как только задана матрица факторных нагрузок. Он отражает степень качества представления данной системой факторов системы исходных параметров. После того, как критерий построен, задача о нахождении матрицы факторных нагрузок ставится как экстремальная задача построенного критерия. Таким образом, формально факторный анализ – это несколько критериев качества матрицы факторных нагрузок и набор алгоритмов поиска экстремумов этих критериев.
3.2.1. Виды факторного анализа Почти все алгоритмы факторного анализа – это простейшие итерационные процедуры поиска экстремума. Довольно часто они обеспечивают достижение лишь локального экстремума соответствующего критерия. Более того, эти алгоритмы не всегда являются, строго говоря, сходящимися, а если сходятся, то сходимость у них очень медленная. Критерии формализуют различные содержательные представления о том, что означает хорошее сжатие информации. Поэтому на практике оказывается полезным подход к обработке материала сразу несколькими методами одновременно. Наличие большого сходства между результатами в этом случае, дает возможность говорить о том, что сжатое представление действительно отражает существо представленной информации, представленной в этом материале. Полезно также сравнивать результаты обработки различными алгоритмами, реализующими поиск экстремума одного и того же критерия. Сходство результатов есть выражение надежности проведенных преобразований. Пусть исследователь располагает совокупностью из N Информацию в этом случае можно представить в виде таблицы чисел: X 11 X22............ X 1 n XN 1 X N 2............ X Nn Иногда изучаемое явление не может быть представлено как совокупность объектов. Тогда исследуют состояние явления на ряд моментов времени. В этом случае строки - это множество временных интервалов (годы, кварталы и т.д). Столбцы таблицы - соответствуют признакам, наиболее существенно характеризующим явление. Если строки матрицы - множества объектов, то это ряды, характеризующие изменения явления в пространстве, если же строки соответствуют временным интервалам, то признаки заданы рядами динамики. Информационный массив, представленный двухмерной таблицей данных, называется матрицей данных. Исследователя в процессе факторного анализа может интересовать: - изменение значений признаков, описывающих один объект во времени; - различие множества объектов по набору признаков; - изменение одного признака во времени и пространстве. Таким образом, появится цепочка: признак - объект - время. В факторном анализе ее принято называть кубом данных. Чаще изучают двухмерные срезы куба данных. Их называют матрицами данных. Существуют разные виды факторного анализа различаемые в зависимости от вида двухмерных срезов: R, Q, O, P, S и T - анализы. 1. R - анализ. Изучается вариация признаков (столбцы) от объекта к объекту (строки). Итог - определяются признаки со сходным характером вариации, составляющие основу факторов. 2. Q - анализ. Матрицу данных из R - анализа транспонируют (теперь - столбцы - объекты - строки - признаки) Объекты - теперь переменные, значения которых изменяются от признака к признаку. 3. P - анализ. Столбцы - признаки, строки - время. Здесь факторы - некие обобщенные параметры, хорошо описывающие вариацию. 4. О - анализ. Матрица данных транспонированная из Р - анализа. Выявленные факторы трактуются здесь как периоды. Интересен O - анализ в первую очередь для историков. 5. S - анализ. Столбцы - объекты наблюдения, строки - временные интервалы. В такой постановке задача факторного анализа позволяет разрабатывать динамическую типологию объектов наблюдения, т.е. выявлять группы объектов со сходным типом изменений во времени. 6. Т - анализ. Столбцы - временные интервалы, строки - объекты наблюдения, признак фиксирован. Служит для выявления периодов времени с характерным для каждого периода распределением значений исследуемого признака по объектам наблюдения. Сегодня доминирует R - анализ, меньше применяется Q и очень редко P - анализ. Остальные схемы факторного анализа пока детально не исследовались. Определив вид матрицы исходных данных, переходят к формированию информационного массива: - определяют список исследуемых переменных; - устанавливают объекты наблюдения, т.е. список объектов. Набор признаков должен определяться опытным специалистом и включать признаки, несущие самую существенную информацию об исследуемом явлении. При отборе признаков исследователь в неявной форме производит взвешивание различных характеристик явления. Исходно набирают большое число признаков, затем проводят их “чистку” (например, исходно было выделено 450 переменных, затем осталось 200. Это число получают обычно после консультации с экспертами). Проблема доступности информации существенно осложняют работу в факторном анализе. Не всегда доступно то, что необходимо иметь для исследования. Если адекватность показателя сомнительна, то лучше привлечь несколько дополнительных вместо него. Важна очень надежность и сопоставимость показателей (например, денежный доход в расчете на душу населения как характеристика уровня жизни занижает уровень стран запада относительно США, т.к. уровень общественных неоплачиваемых услуг выше в Европе, чем в США). Далее, не следует включать в анализ линейно взаимосвязанных (по способу расчета) признаков, т.к. это ведет к тривиальным выводам (например, не следует включать переменные xj и D xj = xjt - xjt -1). Факторный анализ изучает следующие типы признаков: 1. Структурные признаки, отображающие свойства объекта в абсолютном или относительном выражении; 2. Динамические признаки, характеризующие изменения свойств во времени; 3. Характеристики отношений - признаки, которые описывают взаимосвязи между объектами. { Xjkl }, где j - индекс признака, а kl - индексы объектов. Выявленные факторы интерпретируются как основные аспекты взаимоотношений между объектами; 4. Суджестивные признаки - субъективные оценки тех или иных явлений. (Например, при исследовании уровня жизни вводят субъективные оценки благосостояния, при миграции вводят субъективные оценки степени удовлетворения запросов населения и т.д.); 5. Качественные признаки. Факторный анализ только начинает их изучать. Разрабатывают специальные методы. (Пример качественных признаков - ответы на вопросы анкеты при опросе покупателей. Покупатель характеризует обувь: качество кожи, высоту каблука, цвет, и т.д. Задача состоит в выявлении небольшого числа компонентов, типичных сочетаний частных потребительских свойств (факторов), которые характеризуют покупательские предпочтения); 6. При проведении факторного анализа необходимо помнить об уровне агрегирования данных (данные за год или месяц и т.д., данные по стране или области и т.д.) и составе наблюдений (перечень объектов или временных интервалов, по которым идет наблюдение). При этом обобщать результаты полученные по отдельным районам нельзя, т.к. в целом по стране могут быть получены иные выводы. Процедуры факторного анализа начинаются с преобразования матрицы исходных данных. Смысл этого преобразования заключается в том, чтобы ослабить влияние экстремальных значений признаков на результаты расчетов, сделать сопоставимыми изменения значений признака на разных участках шкалы его значений. Влияние характера распределения на результаты расчетов весьма велико, поэтому особо следует рассмотреть вопрос о преобразовании для каждого признака в отдельности. В социально-экономических явлениях преобладают ряды, имеющие правую скошенность (т.е. резкий спад частот с ростом значения признака). При работе с такого рода распределениями часто бывает удобно преобразование к логарифмической шкале (переход от xj к lg xj уменьшает интервал по мере роста xj). Признаки, которые отобраны для исследования, как правило, имеют различную размерность и единицу масштаба измерения. Для их сопоставления и устранения влияния размерности матрицу исходных данных нормируют. Существуют различные способы нормирования. Например, приведение к стандартной форме:
где xij - значение j -ого признака i -ого объекта, Возможны и такие преобразования:
Нормирование - последнее преобразование исходной матрицы, непосредственно предшествующее обработке методами факторного анализа. Обозначим полученную матрицу из нормированных показателей через ú ú Zij ú ú. Если в качестве переменной выступает объект (Q - анализ), не имеющий определенной единицы измерения, то понятие среднего значения здесь не поддается интерпретации (среднее фигурирует при нормировании). Поэтому в Q - анализе вместо коэффициента корреляции используют специально разработанные коэффициенты, измеряющие степень сходства двух объектов по характеру их значений от признака к признаку и по уровню проявления одноименных признаков на этих объектах (пользуется евклидовым расстоянием, например, между векторами-столбцами Xj и Xk, определяющими объекты:
В факторном анализе исходят из того, что признаки, входящие в исследуемый набор, коррелированны. В то же время элементы матрицы корреляций не равны 0 и 1, т.е. ни один из признаков полностью не определяет объект. Наличие корреляций между признаками означает, что существует некий не включаемый в набор скрытый (латентный) параметр, оказывающий влияние на коррелированные признаки. Такого рода скрытые параметры принято называть общими факторами. Факторный анализ занимается их выявлением. Итак Zj может быть представлен как функция небольшого числа общих факторов F 1, F 2, …, Fm и характерного фактора Vj Zj = f (F 1, F 2,.., Fm, Vj) (3.1) Термин общий означает, что каждый Fp (p = 1, 2, …, m) имеет существенное значение для анализа всех переменных Zj (j = 1, 2, …, n), т.е. Fp - общий для всех Zj. Характерный означает, что изменение в факторе Vj изменяет значение только соответствующей переменной Zj. Он отражает специфику, которая не может быть выражена через общие факторы. Методы, основанные на моделях такого типа, различаются ограничениями, накладываемыми на величины Fp, р = 1, 2, …, m и тем, в каком смысле понимается не существенность величин V 1, V 2,..., Vn. Уравнение (3.1), дополненное ограничениями, накладываемыми на факторы, называют моделью. В общем случае в правой части ни коэффициенты, ни факторы не являются известными. Обычно методы факторного анализа рассматривают как аппроксимационные. Некоторые предположения факторного анализа связаны с допущением о линейности его основной модели:
Здесь Zj зависит от общих факторов и характерного фактора. Систему уравнений (3.2) называют факторным отображением. Коэффициенты при факторах называют факторными нагрузками, которые показывают значимость каждого из факторов для j -ого признака. Допущение о линейности взаимосвязей могут вызывать сомнения. Однако модель факторного анализа есть первое приближение к отражению реальных процессов и при ее оценке следует судить о ней по тому, насколько она экономична и эффективна. Запишем выражение для j -ого параметра i -ого объекта:
Под Fpi в (4.3) понимают случайные величины, которые считают нормально распределенным. Полагают, что характерные факторы независимы как между собой, так и по отношению к общим факторам. Из предположения о том, что факторы нормально распределенные независимы случайные величины следует предположение о том, что Zj имеют многомерное нормальное распределение. Для оценки n х m нагрузок общих факторов существуют различные методы. Для вычисления факторных нагрузок используют матрицы коэффициентов корреляции между параметрами. В отличие от регрессионного анализа, где набор независимых параметров предполагается измеряемым в действительности, в факторном анализе эти параметры являются гипотетическими и могут быть оценены лишь при последующем анализе. Процедуры, направленные на получение факторных решений в смысле (3.2) оперируют корреляционными матрицами; при этом корреляция понимается как математическое, а не статистическое понятие. Проблема статистической достоверности здесь игнорируется. Когда возникает вопрос о статистической достоверности, то делаются специальные предположения о характере функций распределения факторов и наблюдаемых параметров. Согласно модели, представленной выше дисперсия параметра может быть выражена через факторы:
Тогда, используя (3.3) и (3.4), получим:
Так как дисперсия параметра, заданного в стандартном виде, равна 1 и все параметры заданны в стандартном виде, а характерные факты не коррелированны с общими и общие не коррелируют между собой, то:
Члены в правой части представляют доли дисперсии параметра Zj приходящегося на соответствующие факторы. Например, aj 22 есть вклад фактора F 2 в дисперсию Zj. Полный вклад Up фактора Fp в суммарную дисперсию параметров определяется выражением:
а полный вклад всех общих факторов в суммарную дисперсию параметров равен:
Из (3.5) следует понятие общность параметра Zj:
и характерность - вклад характерного фактора. Иногда характерность разбивают на две части: специфика параметра, связанная с действительной спецификой параметра и оставшаяся доля - дисперсия ошибки или ненадежность (связана с ошибкой измерения). Тогда суммарная дисперсия будет:
Методы факторного анализа позволяют получать для каждого параметра hj 2 и dj 2. Затем dj 2 разбивают на bj 2 и lj 2. Для этого есть специальные приемы. Можно записать выражения для составляющих полной дисперсии параметра:
Выразив параметры через факторы, перейдем к факторизации данных. Пользуясь (2) запишем для каждого Zj выражения: Z1 = a11F1 + a12F2 +...+ a1mFm + d1 V1
Zn = an1F1 + an2F2 +...+ anmFm + dn Vn Эта система называется факторным отображением. В (3.7) общие факторы могут быть как коррелированны так и нет, а характерные факторы всегда считаются некоррелироваными между собой и с общими факторами. В уравнении некоторые коэффициенты могут быть равны 0. Таблица коэффициентов корреляции между параметрами и факторами называется факторной структурой. Из (3.7) можно перейти к (3.8), умножив любое из уравнений на соответствующие факторы, произведя суммирование по N и разделив на N:
Иногда под факторной структурой понимают таблицу коэффициентов корреляции параметров только с общими факторами т.е. таблицу Если общие факторы не коррелированны между собой, то уравнение (3.8) имеет вид:
После получения факторного отображения необходимо выяснить, насколько адекватно оно описывает корреляции между параметрами. Для этого считают остаточные коэффициенты корреляций как разность между выборочным коэффициентом корреляции и вычисленным. Иногда используют такой критерий:
где: d - стандартное отклонение совокупности остатков. Если d много больше чем В факторном анализе существует проблема неопределенности моделей. Она означает неоднозначность факторных нагрузок ajp и имеет своей причиной то, что факторное решение определяет m -пространство, a не определяет базиса в нем, следовательно, не определяет в нем положение факторов. Большинство вычислительных процедур факторного анализа дают неоднозначное решение для факторных нагрузок (исключение составляет метод главных компонент). Существует более десятка методов факторного анализа. Некоторые из них имеют историческую ценность, другие пригодны только для частных задач, третьи с успехом могут быть применены на практике в самых различных сферах. Появление ЭВМ открыло широкие перспективы использования методов факторного анализа. Наибольшее распространение сегодня получили методы: метод главных компонент, метод максимального правдоподобия, центроидный метод, компонентный анализ. При выборе метода в первую очередь руководствуются особенностями изучаемого объекта.
3.2.2. Метод главных компонент. В этом методе каждый последующий выделенный фактор дает меньший вклад в суммарную общность, чем предыдущий. Это означает, что на первый фактор приходиться максимально возможная доля суммарной дисперсии. Второй фактор учитывает максимум дисперсии в подпространстве, которое получиться после исключения первого фактора и т.д. По существу первый фактор здесь является генеральным. В методе главных компонент могут быть получены факторы, которые могут иметь отрицательные коэффициенты. Интерпретация таких факторов достаточно проста. Они определяют как бы две противоположности, например, экономическую депрессию и экономический подъем. Метод главных компонент не требует, чтобы все элементы корреляционной матрицы были положительными, т.е. он пригоден для любых корреляционных матриц.
3.2.3. Центроидный метод. Долгое время был одним из самых популярных методов, т.к. был наименее трудоемким. Как и в предыдущем методе каждый последующий фактор (центроид) должен “оттягивать” на себе максимум дисперсии. Однако этот метод не дает единственного решения.
3.2.4.Метод максимального правдоподобия. Этот метод дает возможность, задавшись числом общих факторов, найти факторное решение и значение общностей. Для проверки гипотезы о числе факторов в метод включен статистический тест оценки достоверности. Получаемые в методе максимального правдоподобия факторы не “оттягивают” на себя максимум суммарной дисперсии, а сам метод не позволяет однозначно определить пространство общих факторов. Это означает что, чтобы зафиксировать конкретное решение, необходимо ввести дополнительное условие.
|

 наблюдений над состоянием изучаемого явления. Явление описано набором из n признаков
наблюдений над состоянием изучаемого явления. Явление описано набором из n признаков 

 - среднее арифметическое значение j -ого признака, Sj - среднеквадратичное отклонение j -ого признака (Sj 2 - дисперсия j -ого признака).
- среднее арифметическое значение j -ого признака, Sj - среднеквадратичное отклонение j -ого признака (Sj 2 - дисперсия j -ого признака). или
или или
или 
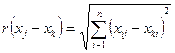 ).
). (3.2)
(3.2) (3.3)
(3.3)
 (3.4)
(3.4)

 (3.5)
(3.5)
 ,
,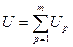
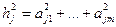
 (3.6)
(3.6) (3.7)
(3.7)
 (3.8)
(3.8)
 (3.9)
(3.9) .
. (3.10)
(3.10) ,
,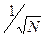 , то какие-то связи между параметрами остались неучтенными и модель, следовательно, нуждается в модификации. Если наоборот (значительно меньше
, то какие-то связи между параметрами остались неучтенными и модель, следовательно, нуждается в модификации. Если наоборот (значительно меньше 


