Составим таблицу дисперсионного анализа для проверки статистической значимости уравнения множественной регрессии и его показателя тесноты связи на уровне значимости
Задача дисперсионного анализа состоит в проверке нулевой гипотезы о статистической незначимости уравнения регрессии в целом и показателя тесноты связи. Анализ выполняется при сравнении фактического и табличного (критического) значений F - критерия Фишера
где
Результаты дисперсионного анализа представлены в таблице 2.
Таблица 2– Дисперсионный анализ
Сравнивая Вероятность ошибки при отклонении нулевой гипотезы не превышает 5 %, что является достаточно малой величиной.
|
и 
определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:
, (3.16)
– число единиц совокупности;
– число факторов в уравнении линейной регрессии;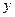
– фактическое значение результативного признака;
– расчетное значение результативного признака.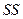
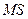
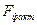
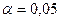
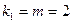
, (3.17)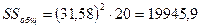
, (3.18)
, (3.19)
, (3.20)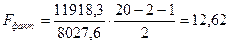
и сделать вывод о статистической значимости уравнения регрессии в целом и значения 
, так как они статистически надежны и сформировались под систематическим действием неслучайных причин.
