Построим уравнение множественной регрессии в стандартизованной и естественной форме
Линейное уравнение множественной регрессии у от х1 и х2 имеет вид:
Для расчета его параметров применим метод стандартизации переменных и построим искомое уравнение в стандартизованном масштабе:
Расчет
Получим уравнение
Для построения уравнения в естественной форме рассчитаем
Значение
Рассчитаем средние коэффициенты эластичности для определения относительной силы влияния
С увеличением средней заработной платы х1 на 1% от ее среднего уровня средний душевой доход у возрастает на 1, 16 % от своего среднего уровня; при повышении среднего возраста безработного Очевидно, что сила влияния средней заработной платы 2. Линейные коэффициенты частной корреляции рассчитываются по рекуррентной формуле:
При сравнении значений коэффициентов парной и частной корреляции приходим к выводу, что из-за слабой межфакторной связи(
Расчет линейного коэффициента множественной корреляции выполним с использованием коэффициентов
Зависимость – средней заработной платы; – среднего возраста безработного. Прочие факторы, не включенные, составляют соответственно 28 % от общей вариации.
|

 (3.1)
(3.1) (3.2)
(3.2) -коэффициентов выполним по формулам:
-коэффициентов выполним по формулам: , (3.3)
, (3.3) , (3.4)
, (3.4)


 и
и  используя формулы для перехода от
используя формулы для перехода от  к
к  :
: , (3.5)
, (3.5) , (3.6)
, (3.6)

 определим из соотношения
определим из соотношения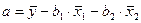 , (3.7)
, (3.7)

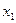 и
и 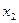 на
на 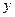 :
: , (3.8)
, (3.8) %
% %
% оказалась большей, чем сила влияния среднего возраста безработного
оказалась большей, чем сила влияния среднего возраста безработного  и
и 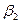 .
.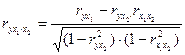 , (3.9)
, (3.9) , (3.10)
, (3.10)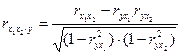 , (3.11)
, (3.11)


 ) коэффициенты парной и частной корреляции отличаются незначительно: выводы о тесноте и направлении связи на основе коэффициентов парной и частной корреляции совпадают:
) коэффициенты парной и частной корреляции отличаются незначительно: выводы о тесноте и направлении связи на основе коэффициентов парной и частной корреляции совпадают:
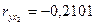
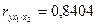


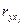 и
и  :
: , (3.12)
, (3.12)



