Гиперболическая модель
Регрессия в виде равносторонней гиперболы имеет вид:
 , (2.15) , (2.15)
Чтобы оценить параметры a и b, приведем модель к линейному виду, заменив 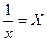 . .
Тогда
 , (2.16) , (2.16)
Применяя метод МНК (метод наименьших квадратов), получаем систему нормальных уравнений:
 , (2.17) , (2.17)
Для расчета параметров составим таблицу 2.
По исходным данным рассчитаем    
Система нормальных уравнений составит:
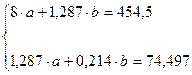
Решим ее методом определителей: определитель системы  равен: равен:
  , (2.18) , (2.18)
  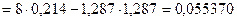
  , (2.19) , (2.19)
 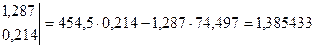
Таблица 2– Вспомогательная расчетная таблица
| Номер региона
|

|
|

|

|

|

|

|

|

| |
| 4, 5
| 68, 8
| 0, 222
| 0, 0494
| 15, 289
| 68, 93
| -0, 13
| 0, 02
| 0, 187
| |
| 5, 9
| 58, 3
| 0, 169
| 0, 0287
| 9, 881
| 58, 51
| -0, 21
| 0, 04
| 0, 360
| |
| 5, 7
| 62, 6
| 0, 175
| 0, 0308
| 10, 982
| 59, 68
| 2, 92
| 8, 50
| 4, 657
| |
| 7, 2
| 52, 1
| 0, 139
| 0, 0193
| 7, 236
| 52, 46
| -0, 36
| 0, 13
| 0, 698
| |
| 6, 2
| 54, 5
| 0, 161
| 0, 0260
| 8, 790
| 56, 89
| -2, 39
| 5, 71
| 4, 384
| |
| 6, 0
| 57, 1
| 0, 167
| 0, 0278
| 9, 517
| 57, 95
| -0, 85
| 0, 73
| 1, 492
| |
| 7, 8
|
| 0, 128
| 0, 0164
| 6, 538
| 50, 35
| 0, 65
| 0, 42
| 1, 270
| |
| 8, 0
| 50, 1
| 0, 125
| 0, 0156
| 6, 263
| 49, 72
| 0, 38
| 0, 15
| 0, 760
| 
| 51, 3
| 454, 5
| 1, 287
| 0, 2140
| 74, 497
| 454, 50
| 0, 00
| 15, 69
| 13, 807
|
 , (2.4) , (2.4)
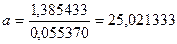
  , (2.21) , (2.21)
  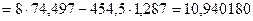
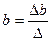 , (2.6) , (2.6)
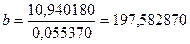
Получаем уравнение регрессии:

Чтобы рассчитать ошибку аппроксимации, найдем расчетные значения  , подставляя в уравнение регрессии соответствующие значения , подставляя в уравнение регрессии соответствующие значения  . .
Для оценки тесноты связи найдем индекс корреляции:
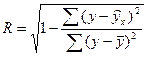
Остаточная сумма квадратов составит:
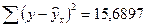
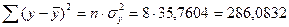
Следовательно, индекс корреляции составит:
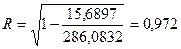
Коэффициент детерминации для уравнения гиперболы равен:
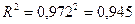
 критерий Фишера будет равен: критерий Фишера будет равен:
 , (2.22) , (2.22)
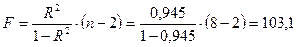
Табличное значение  критерий Фишера при числе степеней свободы 1 и 6 и уровне значимости 0, 05 составит: критерий Фишера при числе степеней свободы 1 и 6 и уровне значимости 0, 05 составит:  , то есть фактическое значение , то есть фактическое значение  критерия превышает табличное, и можно сделать вывод, что уравнение регрессии статистически значимо. критерия превышает табличное, и можно сделать вывод, что уравнение регрессии статистически значимо.
Ошибки аппроксимации для каждого наблюдения определяются как
 %, (2.14) %, (2.14)
Средняя ошибка аппроксимации  находится, как средняя арифметическая простая из индивидуальных ошибок: находится, как средняя арифметическая простая из индивидуальных ошибок:
 % %
Ошибка аппроксимации показывает соответствие расчетных  и фактических и фактических  данных. данных.

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|

Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|

Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|
Закон Гука при растяжении и сжатии
Напряжения и деформации при растяжении и сжатии связаны между собой зависимостью, которая называется законом Гука, по имени установившего этот закон английского физика Роберта Гука в 1678 году...
Характерные черты официально-делового стиля Наиболее характерными чертами официально-делового стиля являются:
• лаконичность...
Этапы и алгоритм решения педагогической задачи Технология решения педагогической задачи, так же как и любая другая педагогическая технология должна соответствовать критериям концептуальности, системности, эффективности и воспроизводимости...
|
Словарная работа в детском саду Словарная работа в детском саду — это планомерное расширение активного словаря детей за счет незнакомых или трудных слов, которое идет одновременно с ознакомлением с окружающей действительностью, воспитанием правильного отношения к окружающему...
Правила наложения мягкой бинтовой повязки 1. Во время наложения повязки больному (раненому) следует придать удобное положение: он должен удобно сидеть или лежать...
ТЕХНИКА ПОСЕВА, МЕТОДЫ ВЫДЕЛЕНИЯ ЧИСТЫХ КУЛЬТУР И КУЛЬТУРАЛЬНЫЕ СВОЙСТВА МИКРООРГАНИЗМОВ. ОПРЕДЕЛЕНИЕ КОЛИЧЕСТВА БАКТЕРИЙ Цель занятия. Освоить технику посева микроорганизмов на плотные и жидкие питательные среды и методы выделения чистых бактериальных культур. Ознакомить студентов с основными культуральными характеристиками микроорганизмов и методами определения...
|
|

 , (2.15)
, (2.15)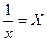 .
. , (2.16)
, (2.16) , (2.17)
, (2.17)



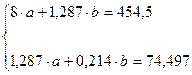
 равен:
равен:
 , (2.18)
, (2.18)

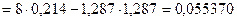


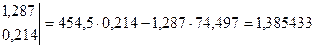








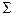
 , (2.4)
, (2.4)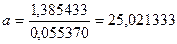

 , (2.21)
, (2.21)

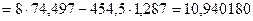
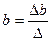 , (2.6)
, (2.6)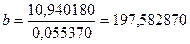

 , подставляя в уравнение регрессии соответствующие значения
, подставляя в уравнение регрессии соответствующие значения  .
.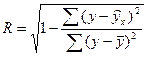
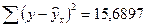
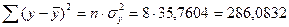
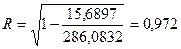
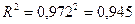
 критерий Фишера будет равен:
критерий Фишера будет равен: , (2.22)
, (2.22)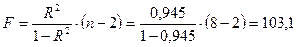
 , то есть фактическое значение
, то есть фактическое значение  %, (2.14)
%, (2.14) находится, как средняя арифметическая простая из индивидуальных ошибок:
находится, как средняя арифметическая простая из индивидуальных ошибок: %
% данных.
данных.


