Определим методом наименьших квадратов параметры уравнения линейной регрессии
Параметры a и b линейной регрессии
По исходным данным рассчитаем Таблица 1– Вспомогательная расчетная таблица
Система нормальных уравнений составит:
Получаем уравнение регрессии:
Величина коэффициента регрессии Подставив в уравнение значения 2. Найдем показатели тесноты связи линейной модели: Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции Как известно, линейный коэффициент корреляции находится в границах:
–1 ≤
Если коэффициент регрессии Если коэффициент регрессии Линейный коэффициент корреляции равен:
Вывод: связь между признаками очень высокая обратная, так – 0, 9 < Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции Коэффициент детерминации характеризует долю дисперсии результативного признака у, объясняемую регрессией, в общей дисперсии результативного признака:
Соответственно величина Коэффициент детерминации –
То есть вариация Величина коэффициента детерминации является одним из критериев оценки качества линейной модели. Чем больше доля объясненной вариации, тем соответственно меньше роль прочих факторов и, следовательно, линейная модель хорошо аппроксимирует исходные данные, и ею можно воспользоваться для прогноза значений результативного признака.
|

 рассчитываем в результате решения системы нормальных уравнений относительно a и b.
рассчитываем в результате решения системы нормальных уравнений относительно a и b. (1.1)
(1.1)



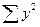

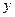




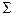
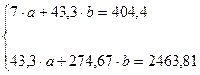
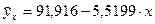
 означает, что с ростом заработной платы на 1 тыс. руб. доля расходов на покупку продовольственных товаров снижается в среднем на 5, 5 %–х пункта.
означает, что с ростом заработной платы на 1 тыс. руб. доля расходов на покупку продовольственных товаров снижается в среднем на 5, 5 %–х пункта. не имеет экономического смысла.
не имеет экономического смысла. .
. > 0, то 0 ≤
> 0, то 0 ≤  , (1.2)
, (1.2) , (1.3)
, (1.3)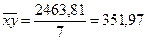
 , (1.4)
, (1.4)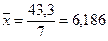
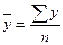 , (1.5)
, (1.5)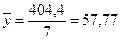
 , (1.6)
, (1.6)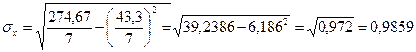
 , (1.7)
, (1.7)
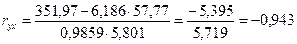
 < –0, 99
< –0, 99 называемый коэффициентом детерминации.
называемый коэффициентом детерминации. , (1.8)
, (1.8) характеризует долю дисперсии
характеризует долю дисперсии 
 . На долю прочих факторов, не учитываемых в регрессии, приходится 11, 08 %.
. На долю прочих факторов, не учитываемых в регрессии, приходится 11, 08 %.


